日本数学協会
小学校から大学までの数学教育が数学嫌いをつくっているという批判がある一方で、たくさんの数学の入門書が書店の棚を飾っています。
考える楽しみを与えてくれる数学、様々な分野に応用されている数学。こうした数学の持つ面白さ、美しさや不思議さを味わうことのできる場が必要とされています。
とりわけ、数学を学ぶ楽しさを語り合うことができる場、自らの発見を語ることのできる場、
数学と関連する諸分野の方たちと互いに語り合うことができる場が、今まで以上に必要とされています。
こうした場をつくり、皆で数学を楽しみ、数学文化を豊かに育むことを願い、日本数学協会を設立いたしました。
たくさんの方々が入会され、我が国の数学文化がさらに豊かになることを希望しております。
会長 上野 健爾 .
❖❖❖ 日本数学協会 Zoom講義 ❖❖❖
<テーマ> 【 塵劫記をめぐって 】
講義Ⅲ・Ⅳ 「『塵劫記』発刊の目的と対象」
* 講 師: 曽我 昇平 氏 (愛知学院大学文学部非常勤講師、四日市大学関孝和数学研究所所員)
* 開講日: 7月20日(日)・8月24日(日)
※詳しくは、「講義のご案内」ページをご覧ください。
上記日程以降も複数の専門家によるリレー式で開催
❖❖❖ 日本数学協会 Zoom講義 ❖❖❖
【テーマ】 < 代数幾何入門 >
* 講 師: 上野 健爾 氏(四日市大学 関孝和数学研究所)
※全10回、詳しくは「講義のご案内」ページをご覧ください
❖❖❖ 日本数学協会 Zoom講義 ❖❖❖
【テーマ】 『 文化のなかの数学 』
* 講 師: 三浦 伸夫 氏(神戸大学名誉教授)
* 開講日: 5月18日(日)・6月22日(日)・7月27日(日)・9月21日(日)・10月19日(日)変更 10月26日(日)
※全5回、詳しくは、「講義のご案内」ページをご覧ください。
今年度の企画紹介
1. 三浦 伸夫氏(神戸大学名誉教授)
「数学文化史」(全5回)
毎回異なる題材を取り上げ、西洋数学を文化史のなかで捉える
・ アラビア数字の伝承と数的素養
・ 数学讃歌
・ 技術者・芸術家は読み書きができなければならない
・ 数学器具の成立と展開
・ 数学者と共通語
高度な数学には言及せず文化史、交流史、美術史、教育史などに関心のある方にも参考になるであろう
2. 上野 健爾氏(四日市大学関孝和数学研究所)
「代数幾何入門」(全10回)
代数的な観点と複素解析的な観点を交えた形で代数幾何の入門講義を行う
3. 上野 健爾氏
「ガロアを読む3」(全3回)
ガロアが決闘の前夜に書いたシュヴァリエ宛の手紙の講読を行う
4. リレー講座
「塵劫記をめぐって」
2027年は吉田光由が『塵劫記』を出版してから400年の記念すべき年になります。その準備として『塵劫記』と著者の吉田光由をめぐって専門家の方々の講義を予定しています
以上
日本数学協会は、第24回総会での決議で解散することになりました。(2024年7月27日)
ただし、Zoom講義のみ活動を継続します。(最長3年)
そして、新たに「Zoom講義会員」を新設します。(年会費4,000円)
ご案内は当ホームページ内『入会のご案内』ページにあります。
※ Zoom講義会員は、会員期間中に開催するZoom講義を無料で聴講できます。
日本数学協会がこれまでに出版した『数学文化』のバックナンバーを販売しています。
詳しくは、「機関誌『数学文化』」のページをごらんください。
※在庫数には限りがあります
❖❖❖ 日本数学協会 Zoom講義 ❖❖❖
<テーマ> 【 塵劫記をめぐって 】
* 講 師: 小川 束 氏 (四日市大学 関孝和数学研究所)
* 開講日: 5月11日(日)・6月8日(日)
※上記日程以降も複数の専門家がリレーして開催を予定。詳しくは、「講義のご案内」ページをご覧ください。
❖❖❖ 日本数学協会 Zoom講義 ❖❖❖
【新テーマ】 < ガロアを読む 2 >
* 講 師: 上野 健爾 氏(四日市大学 関孝和数学研究所)
* 開講日: 2025年2月2日(日)・ 2月23日(日)
※詳しくは、「講義のご案内」ページをご覧ください。
❖❖❖ 日本数学協会 Zoom講義 ❖❖❖
【新テーマ】 『 複素解析入門 』
* 講 師: 上野 健爾 氏(四日市大学 関孝和数学研究所)
* 開講日: 2024年9月15日(日)・ 9月22日(日) ・ 10月6日(日)・ 10月20日(日) ・ 11月3日(日)
※詳しくは、「講義のご案内」ページをご覧ください。
第24回総会議事録
至 2024年7月27日(土)
総会のご報告
第24回総会が、2024年7月27日(土)に行われました。
2023年度事業活動報告・同収支決算、2024年度活動計画(案)・同役員/委員会について、
慎重にご審議頂き、無事原案どおり全て異議なく承認されました。
また、解散に伴う清算人の選出および財産処分の方法について、
慎重にご審議頂き、無事原案どおり全て異議なく承認されました。
日本数学協会解散に当たっての財産処理方法は以下のとおりです。
「日本数学協会解散時において残存する資産については、日本数学協会解散後のZOOM講義の運営主体に移管する」
以上、ご報告いたします。
(議事録を議事録署名人の記名押印後に掲載します)
第24回総会を開催します
総会へのご出席をお願いします.
※ 出席/欠席のご連絡は,7月22日(月)までにE-Mail,FAXまたは郵便で事務局宛にお願いします.
ご都合によりご参加できない会員の方は,「委任状」のご提出をお願いします.【委任状】第24回総会.docx
・日 時 2024年7月27日(土) 13:30~14:15
(総会終了後に講演会を開催します)
・議 題 (1)2023年度事業活動報告・同収支決算(案)について
(2)2024年度以降の活動計画(案)について
(3)2024年度以降の役員・委員会について
(4)解散にともなう清算人の選出、および財産処分の方法について
(5)その他
・会 場 ① Zoom中継
② トモエ算盤株式会社 2階会議室 (東京都新宿区若葉1丁目10番地)
JR・東京メトロ「四ツ谷駅」下車
※ 会場の収容人数の関係で「②」(対面)の参加は先着順になります(約30名)
②の会場アクセス( https://www.soroban.com )← 〔会社案内〕タブをクリックして移動後[アクセス]をクリックしてください
・参加申込み 下記要領でメールにてお申し込みください
<メール連絡の様式>
あて先:sugakubunka@gmail.com
件名: 総会について
本文: <出席の場合>
(1)参加者氏名
(2)出席する会場 (①Zoom または ②対面 のどちらかを記載する)
(3)講演会に 出席する/欠席する
(4)Zoom講義会員に なる/ならない
本文に上記4項目は必ず記載してください
※ 申込み時のメールアドレス宛にZoomに参加するためのリンク情報(URL、ミーティングID、パスコード)を返信いたします。
<欠席の場合>
委任状を提出してください 【委任状】第24回総会.docx
◎総会終了後に講演会を開催いたします
講演会: 14:30~15:30
演 題: 「『塵劫記』刊行400年を迎えて」
講演者: 小林 龍彦 氏 (日本数学史学会会長・前橋工科大学名誉教授)
参加費: 正会員:無料 非会員:1,000円
申込み: 正会員:総会への参加申込みに講演会も出席すると記載ください
非会員:Peatix からお申込み
Peatix:< https://peatix.com/event/4051245/view >
※Peatixを Google Chrome で開いた後、イベント検索で探してください
以上
❖❖❖ 日本数学協会 Zoom講義 ❖❖❖
【新テーマ】 『 和算書の楽しみ Ⅱ 』
* 講 師: 菅原邦雄氏(大阪教育大学名誉教授)
* 5月から月1回、全5回の開催を予定しています
※詳しくは、「講義のご案内」ページをご覧ください。
❖❖❖ 日本数学協会 Zoom講義 ❖❖❖
【新テーマ】 『 べき級数から見た複素解析 』
* 講 師: 上野健爾氏(四日市大学 関孝和数学研究所)
* 開講日: 2024年4月14日(日)
※詳しくは、「講義のご案内」ページをご覧ください。
臨時総会のご報告
第23回総会(臨時)が、2024年3月17日(日)にZoom中継で行われました。
2023年度事業活動の中間報告・同収支の中間報告を説明した後、
2024年度以降の事業活動方針案について、会員の意見を求め質疑応答や意向の確認を行った。
今回の方針案を具体的にまとめ、2024年度に開催する総会でその議案を決議することになった。
臨時総会を開催します ≪ Zoom中継 ≫
臨時総会へのご出席をお願いします.
※ 出席/欠席のご連絡は,2月29日(木)までにE-Mail,FAXまたは郵便により事務局宛にお願いします.
ご都合によりご参加できない正会員の方は,「委任状」のご提出をお願いします.第23回総会(臨時)-委任状.pdf
※ 2月29日(木)までにE-Mail,FAXまたは郵便により事務局宛にお願いします.
日 時 2024年3月17日(日) 13:30~14:30
議 題 (1)2023年度(期中)の事業活動報告・同収支報告について
(2)2024年度以降の事業活動について
※ 臨時総会に参加するための Zoomリンク情報は,事務局から後日メールでご連絡いたします.
<メール連絡の様式>
あて先:sugakubunka@gmail.com
件名: 臨時総会
本文: <出席の場合>氏名と参加する旨を記載してください
<欠席の場合>委任状を記載してください(別紙添付でも結構です)
以上
vvv 日本数学協会 Zoom講義 vvv
【新テーマ】 『 複素解析を学ぶための微積分入門 』
* 講 師: 上野健爾氏(四日市大学 関孝和数学研究所)
* 開講日: 2024年1月21日(日)・ 2月4日(日) ・ 2月12日(月・振休) ・ 2月25日(日)・ 3月10日(日) ・ 3月24日(日)
※詳しくは、「講義のご案内」ページをご覧ください。
vvv 日本数学協会 Zoom講義 vvv
【新テーマ】 『 ガロアの「連分数」の論文を読む 』
* 講 師: 上野健爾氏(四日市大学 関孝和数学研究所)
* 開講日: 2023年11月12日(日) ・ 11月19日(日)
※詳しくは、「講義のご案内」ページをご覧ください。
vvv 日本数学協会 Zoom講義Ⅲ vvv
【テーマ】 『 和算書の楽しみ 』
* 講 師: 菅原 邦雄 氏(大阪教育大学名誉教授)
* 開催日: 10月22日(日) ・ 11月26日(日) ・ 12月17日(日) ・ 2024年1月14日(日) ・ 2月11日(日)
※詳しくは、「講義のご案内」ページをご覧ください。
vvv 日本数学協会 Zoom講義Ⅱ vvv
【テーマ】 『 江戸時代の人々の数学の愉しみかた 』
* 講 師: 小川 束 氏(四日市大学関孝和数学研究所副所長,暁学園顧問・同教育研究センター長)
* 開催日: 10月1日(日) ・ 11月5日(日) ・ 12月3日(日) ・ 2024年1月7日(日) ・ 2月4日(日)
※詳しくは、「講義のご案内」ページをご覧ください。
2023年(令和5年)度 年次大会のお知らせ
今年度の年次大会は東京と福井の2ヵ所で開催します。
【 日本数学協会年次大会・東京開催 】
日時:9月2日(土)13:00~16:30
【 日本数学協会年次大会・福井開催 】
日時:10月14日(土)13 : 00~16:00
大会の内容は、下記お知らせのそれぞれのご案内をご確認ください。
2023年(令和5年)度 年次大会 ≪福井大会≫
開催日時:2023年10月14日(土) 13:00~16:00
会場:福井大学文京キャンパス(福井市)/ 総合研究棟Ⅰ(13階)の2階講義室
https://www.u-fukui.ac.jp/cont_about/data/access/
JR福井駅から越前鉄道(私鉄)三国線で「福大前西福井」で下車(10分).
(徒歩で3分)
参加料:日本数学協会会員または高校生以下(500円)、それ以外(1000円)
(1)申し込み締め切り:10月6日(金)
・会場参加希望者およびZoom中継参加希望者は下記Peatix(URL)のよりお願い致します。
https://peatix.com/event/3667697/view
日本数学協会会員(無料) , 非会員(1000円)
*尚、Peatixにてお申し込み頂きました参加費につきましては、
理由の如何を問わず、ご返金できませんことをご承知おきくださいませ。
・会場参加者は当日参加も可(ただし、90名に到達次第〆切)
(2) 問い合わせ先(ただし電話は9月6日以降):
趙 雪梅研究室(福井医療大学)
メール:chou@fukui-hsu.ac.jp
Tel:0776-59-2200 (大学)
講演Ⅰ 「算数学のススメ」 13:00~14:00
黒木哲徳氏(福井大学名誉教授)
その昔、算数は子どもたちの好きな教科のトップでした。いまは、どうでしょうか?
今でも算数は好きな教科のトップなのですが、同時に嫌いな教科のトップでもあります。いまや算数は評価が二極化する教科になってしまったのです。それはなぜか?
一つには子ども達を取り巻く環境が変化し、子どもの認知の受容形態が変わってしまったことにあります。そのために、これまでとは違った算数指導の取り組みが必要なのです。それが算数学です。ここでは、そのさわりだけを少しご紹介しましょう。
<講師紹介>
黒木哲徳さんは、算数・数学の教育研究にかかわり、大学教師を生業とし、半世紀近く越前国福井に住む. 算数学の必要性を唱え、自前の教材で全国の小・中学校での出前授業―なぜか“母を訪ねて三千里”の海の向こうでもちょっぴり教育支援―流れ流れて生まれ故郷の神話の里で慣れない教育行脚―いまは無職. 著書に「入門算数学」(日本評論社)、「算数から数学まで」(日本評論社)、「なっとくする数学記号」(講談社ブルーバックス)など.
講演Ⅱ 「珠算式暗算のススメ」 14:00~14:50
田村聡子氏(大阪市小学校教諭)
小学生にはもちろん、大人にも役に立つ暗算のススメ!
たかが計算、されど計算です.
デジタルの時代だからこそ必要なスマートな頭の体操を!
ソロバンのプロが丁寧に教える、とっておきの暗算方法を修得しませんか。
数字見え方から、珠算式の計算法、さらにはいろんなバリエーションまで、暗算の面白さ
を大いに楽しみましょう。算数の指導にも大いに参考になります.
<講師紹介>
田村聡子さんは多彩な方です. 現在は大阪市の小学校教諭.
そろばん塾や学習塾の経営を経て、途中から小学校の教師を目指す.
小学校では外国語専科や特別支援学級も担任、現在は5年生の担任.
さらには、現在はボーイスカウトの指導者であり、地域では保護司として社会を明るくす
る運動に一翼を担っておられます. エネルギー溢れる教育者です。
ワークショップ:「フレクサチューブとメービウスフラワー」 15:00~16:00
(数学的解説を含む)
伊藤仁一氏(椙山女学園大学教授)
参加者が用意するもの:「空の牛乳パック、折り紙、セロテープ、カッター、カッターパット、ハサミ」
ワークショップの内容:
小学生から大人まで楽しめるやさしいておもしろいワークショップ.
直観幾何学の第一人者伊藤仁一先生の発見学習を体験できる貴重な機会.
小学校・中学校・高校での授業のヒントも得られますよ.
・牛乳パックを使ってフレクサチューブ作成―折ることで表と裏が入れ替わるー
これは正方形4枚をチューブ状につなげたもので、対角線でだけ折り曲げることができる. これを折ることで表と裏が入れ替わる. なんとも不思議、お楽しみを!
・メービウスの帯の輪切りの拡張(秋山仁先生考案)を楽しむ
メービウスの帯を輪に沿って切るとどうなるかはよくある話. ここではそれを拡張した図形の楽しみを満喫しよう. 内容は参加してのお楽しみ!
<講師紹介>
伊藤仁一さんは幾何学者、理学博士. 現在は椙山女学園大学教授、以前の熊本大学教育学部教授時代から「直観幾何学」の研究会を年に1回開催、「直観幾何学」の確立を目指しておられます.「直観幾何学」を道行く一般の人にも説明できるような図形の研究をモットーに、関連する論文多数. 数学教育にも造詣が深く、直観幾何学を用いた発見学習に力を入れておられます. 中学校教科書『日々の学びに数学的な見方・考え方をはたらかせる これからの数学1,2,3』(数研出版)の執筆者の一人.
2023年(令和5年)度 年次大会 ≪東京大会≫
●日時:9月2日(土)13:00~16:30
※ 会場への入場は12:30から可能です。
●会場:喫茶室ルノアール・新宿3丁目ビッグスビル店・貸会議室
※ 会場のURL:https://www.ginza-renoir.co.jp/shopsearch/shops/view/103
※ 最寄り駅は都営地下鉄「新宿三丁目駅」ですが、「新宿駅」の地下街から地上に出ることなく会場へ行くことができます。ただし、地下街には喫茶室ルノアールの他の店舗もありますので、ご注意ください。
●内容:ワークショップ1(13:00~14:30)、ワークショップ2(15:00~16:30)
●会場での参加費:会員は1500円、非会員は2500円
※ 会場での参加費には飲み物代(飲み物はコーヒーか紅茶)が含まれています。
※ 会場でワークショップに参加する場合には、材料費(下記)が別途必要になります。見学するだけの場合には、材料費は不要です。
●Zoomでの参加費:会員は無料、非会員は1000円
●申し込み方法:会場での参加の場合にもZoomでの参加の場合にもPeatix(下記URL)でのお申し込みをお願いいたします。
※ Peatix:https://peatix.com/event/3667697/view
「あやとりであそぼう ~数学の目で見たあやとり~」
長谷川 浩氏(娯楽数学愛好家)
※ 講師の長谷川氏は娯楽数学のウェブサイト「あそびをせんとや」で有名な方で、初期の『数学文化』に連載をなさっていた方です(39号にも寄稿してくださいました)。そんな長谷川氏が近年「パターンあやとり」の研究に力を入れていらっしゃいます。ワークショップ1では、参加者のみなさんに実際にあやとりを取っていただきます。そして、いろいろなあやとりを数学的な目で見比べていただきます。
●追記情報1:長谷川氏がご自身のサイト(下記リンク先)にワークショップの詳しい案内(workshop20230902.pdf)を掲載なさいました。
※ ご参照ください:http://www.lcv.ne.jp/~hhase2/sf1/sf1.html
※ 会場でワークショップ1に参加するには、「あやとり専用の紐」の費用(参加費とは別、現地払い、400円)が必要になります。ただし、紐を持参なさる場合にはその費用は不要です(ワークショップは紐の結び方の説明から始まる予定です)。
●ワークショップ2:
「編み紙工作ワークショップ(理論解説付き)」
堀川 由人氏(大阪大学大学院招聘研究員)
※ 講師の堀川氏は、紙を編んで作る数学アート「懸垂面・螺旋面の変形模型」「立体射影の模型」で有名な方です。ワークショップ2では、参加者のみなさまに実際に紙を編んでいただき、これらの模型の一方(もしくは両方)を工作していただきます。編み紙についての工学的解説や模型の曲面についての数学的解説もありますので、興味がおありの方は(工作の手をやすめて!)解説もお楽しみください。
※ ご参照ください:https://github.com/hyrodium/ElasticSurfaceEmbedding.jl
※ 会場でワークショップ2に参加するには、「懸垂面・螺旋面の変形模型」「立体射影の模型」の少なくとも一方の材料費(参加費とは別、現地払い、一方だと2000円、両方だと4000円)が必要になります。
●追記情報1:堀川氏がでワークショップの材料(キット)の販売を開始なさいました。 Zoomで参加なさる方も制作に参加できますので、下記からお求めください。
「立体射影の模型」<https://
「懸垂面・螺旋面の変形模型」<https://hyrodium.
※ 都合により、「立体射影の模型」のみを工作の対象とすることがありえます。あらかじめご承知おきください。 ← 「懸垂面・螺旋面の変形模型」も実施することになりました。
●注意:今後ワークショップ1、2についての追加情報がある場合には、当協会のホームページや会員向けのメールなどでご報告する予定です。
2023年(令和5年)度 年次大会について〔予告〕
今年度の年次大会は2回開催します。そのおおよその概要をお知らせいたします。
開催日時に関しましては変更がない予定です。
詳細な内容につきましては、仮の部分や変更を含め、
8月7日(月)以降にご案内およびホームページに掲載いたしますのでそちらをご覧ください。
【 日本数学協会年次大会・東京開催 】
<概要>
日時:9月2日(土)13:00~16:30
場所:新宿3丁目ビックスビル店会議室( ㈱ルノアール)
内容:ワークショップ(参加費とは別途、費用が必要となる可能性があります)
その1(13:00~14:30)
「あやとりであそぼう~数学の目で見たあやとり~」
長谷川 浩氏(娯楽数学愛好家)
その2(15:00~16:30)
(仮題)「編み紙工作ワークショップ(理論解説付き)」
堀川 由人氏(大阪大学大学院招聘研究員)
【 日本数学協会年次大会・福井開催 】
<概要>
日時:10月14日(土)13 : 00~16:00
会場 : 福井大学/文京キャンパス(福井市)
内容:講演会&ワークショップ
講演1(13:00~14:00)
「算数学のススメ」
黒木 哲徳氏(福井大学名誉教授)
講演2(14:00~14:50)
「珠算式暗算のススメ」
田村 聡子氏(大阪/小学校教諭)
ワークショップ(15:00~16:00)
「フレクサチューブとメービウスフラワー(数学的解説を含む)」
伊藤 仁一氏(椙山女学園大学教授)
*牛乳パックなどを使って制作します
年次大会について
2023年度の年次大会を8月19日(土)に開催する予定だと総会で発表しましたが、
諸事情により9月以降の開催に変更となりました。
ワークショップやパネルディスカッションを複数の会場、異なる日時で開催することを予定しています。
日程や会場など詳しい内容は、決まり次第ご案内いたします。
第22回総会が2023年5月28日(日)にZoomを利用したオンライン開催で行われました。
2022年度事業活動報告・同収支決算、2023年度事業活動計画・同収支予算について慎重にご審議頂き、無事原案どおり全て異議なく承認されました。
また、2023年度~2025年度の役員選出について、慎重にご審議頂き、無事原案どおり全て異議なく承認されましたのでご報告いたします。
『数学文化』バックナンバー・フェア & 創刊20周年記念トークイベント
2023年5月7日(日)まで書泉グランデ(千代田区神田神保町)で『数学文化』のバックナンバー・フェアを開催しています。
また、4月28日(金)には創刊20周年記念トークイベントも開催します。
『数学文化』創刊20周年記念トークイベント
タイトル 「数学文化とは何か」
* 講 師: 三浦伸夫氏(神戸大学名誉教授)
* 開講日: 2023年4月28日(金) 18:30~20:00
* 会 場:
書泉グランデ7階
* 参加条件: 4月28日までに書泉グランデにて『数学文化』を購入
(購入時に参加券をもらってください)
書泉グランデ様 ↓ ホームページからもご確認ください
https://www.shosen.co.jp/event/7805/

「 くまもと数学秋祭り 」のお知らせ
・主催:NPO法人数学カフェ
・後援:数理女子、日本数学協会
NPO法人数学カフェさん(https://mathcafe.net/)が主催なさる「くまもと数学秋祭り」を日本数学協会が後援することになりました。
2022年11月19日(土)~20日(日)に熊本県熊本市で「くまもと数学秋祭り」が開催されます。
数学ゲーム・折り紙のワークショップ(現地開催、無料)や、
熊本大学・九州大学の研究者による講演会(現地でもオンラインでも参加可能、有料、要事前登録)などがプログラムされています。
プログラムなどの詳細についてはこちら(https://kumamoto.mathcafe.net/)をご覧ください。
日本数学協会員限定で講演会と対談会の録画をYouTubeに公開しています。
YouTubeのURLは、当ホームページのグループスペース内の「特別講義ー講義資料」に載せています。
ログイン後、「特別講義ー講義資料」ページを開いてご覧ください。
第20回 年次大会を開催いたします
2022年度 第20回年次大会 を下記のとおり開催いたします
ご確認の程よろしくお願い申し上げます。
案内チラシ【 2022年度_第20回年次大会チラシ.pdf 】
※ 新型コロナの新規感染者数の状況によってはオンライン開催(Zoom)に変更することがあります
日 時 : 2022年9月18日(日)
13:20~16:30(受付開始12:40)
場 所 : 東京大学(駒場) 数理科学研究科棟 大講義室
(京王井の頭線「駒場東大前」)
参加費 : 会員1,000円 非会員2,000円
(高校生、大学生は無料)
参加申込方法: 下記2通りからお選びください
①当日に会場受付で申込み
②事前にPeatix(*)で申込み(締切:9月13日(火))
< https://peatix.com/event/3312778/view > ※オンライン開催に変更の場合はPeatixによる事前申込みのみになります
*)Peatixとはイベントを告知し、参加を申込みするウェブサービスです
プログラム:
12:40~ 参加受付(開場)
13:20~13:30 挨拶
13:30~14:30 講演 「子どもの算数を数学者が見ると」
谷口 隆氏(神戸大学大学院理学研究科 教授)
14:30~14:50 質疑応答
14:50~15:00 休憩
15:00~16:00 対談 「ことばと算数をめぐって」
谷口 隆氏(神戸大学大学院理学研究科 教授)
広瀬 友紀氏(東京大学大学院総合文化研究科 教授)
16:00~16:30 質疑応答
17:00 退場終了(閉場)
講演会・対談会の内容:
講演会:「子どもの算数を数学者が見ると」 谷口 隆氏
幼い子どもにとって算数をめぐる風景はどんなふうに見えているか、皆さんは考えてみたことがありますか?
子どもの算数を見ていて、次から次へと繰り出される誤答珍答に面食らい、困惑した経験は、多くの方がお持ちかと思います。
一体何をどうするとそんな答えになるのか・・・・・・。
大人の目線ではなく、子どもの目線に合わせて、算数を見てみると意外な世界が広がります。
子どもの算数の世界を一緒に覗いてみませんか?
対談会:「ことばと算数をめぐって」 広瀬 友紀氏/谷口 隆氏
心理言語学の立場から子どもの言語処理に関心のある広瀬教授と数学者である谷口教授が、
「子どもの算数」をめぐって、楽しく、かつ奥深い対談を繰り広げます。
今、いろんな方面で話題になっているお二人の対談が実現しました。乞うご期待!
以上
第21回総会が2022年5月29日(日)に行われました。
今回もZoomを利用したオンライン・リモート開催でした。
2021年度事業活動報告、同収支決算、同じく2022年度事業活動計画、および同収支予算について慎重にご審議頂き、
無事原案どおり、全て承認されましたのでご報告いたします。
第21回総会議事録.pdf
第21回総会および講演会を開催いたします
今年もオンラインミーティングアプリ「Zoom」を使って開催することになりました。
ご都合により、ご参加できない正会員の方は、「委任状」のご提出をお願いいたします。
※ 5月23日(月)までにFAX、E-Mailまたは郵便により事務局宛にお願いいたします。
日 時 : 2022年5月29日(日)
総 会 午後 1時00分 ~ 午後 1時30分
講演会(二部)午後 1時35分 ~ 午後 3時50分
総会 議題 :
(1)2021年度事業活動報告および同収支決算について
(2)2022年度事業活動計画(案)および同収支予算(案)について
(3)その他
総会と講演会に参加するためのZoomミーティングの①URL、②ミーティングID、③パスワードは、メールでご連絡いたします。
つきましては、日本数学協会事務局まで参加申込みのメールを送信してください。
<総会・講演会に参加申込みメール>
Ø あて先:sugakubunka@gmail.com
Ø 件名: 総会の参加について
Ø 本文: 氏名と電話番号だけは必ず記載してください
※送信いただいたメールアドレスに上記①~③のZoomの情報を5月28日までに発信いたします。
総会終了後に講演会を開催いたします。
講演会①: 午後 1時35分 ~ 午後 2時35分
『イエズス会と和算』
曽我 昇平 氏 (愛知学院大学文学部非常勤講師、四日市大学関孝和数学研究所所員)
講演会②: 午後 2時50分 ~ 午後 3時50分
『初等数学を楽しむヒント』
宮永 望 氏 (大学非常勤講師、日本数学協会幹事)
< 講演会参加費 >
正会員:無料 (正会員の方は総会参加の要領でお申込みください)
非会員:1,000円 (非会員の方は Peatix からお申込みください)
Peatix:< https://peatix.com/event/3247097/view>
※Peatixを Google Chrome で開いた後、イベント検索で探してください
URL、IDとパスコードは、参加が確定された方に、メールで連絡します
※ 是非ご参加いただき、今後の活発な活動にご協力をお願いいたします。
諸般の事情により、2022年の新春特別講義は中止いたします。
会長 上野 健爾
多くの参加者が集まり、2講演とも盛況のうちに終えることができました。
後半の演者のHoult 知子氏が、そのときの講演をYouTubeに掲載されていますので、皆様にご紹介いたします。
「そろばん普及活動について」 Hoult 知子氏
第19回年次大会(講演会)をZoom中継で開催いたします。
講演会は、非会員の方も参加可能です。
Ø 日 時: 9月12日(日) 15:00~17:00
Ø 参加費: 正会員=無料 非会員=1,000円
Ø 講演: ①15:00~16:00 ②16:00~17:00
① 「誰も知らない立方体の秘密 ― 直観幾何学への誘い ―」
伊藤 仁一氏 (椙山女学園大学教授)
立方体を中心に、直観幾何学と言えるような研究の中から、いくつかを紹介します。
直観幾何学とは具体的で初等的な幾何の問題を、絵を多用して考える研究と思って下さい。
このような問題を考えることは、数学者やパズル愛好家のみならず、特に発見的学習が推奨されている昨今、中学・高校の数学の先生や、
将来、先生を目指す大学生・大学院生にも有意義だと思います。
具体的には、閉測地線、鋭角三角形分割、通り抜ける小さい穴、変形する多面体、
ビリヤード軌道をブロックする点集合、裏返し等々です。
② 「そろばん普及活動について」 Hoult 知子氏 (そろばん講師 *イギリス在住)
現在イギリスにおいて子供達にそろばん指導を行いながら、Japan Societyのサポートを得てそろばんを学校教育に取り入れてもらえるような普及活動を行っています。
計算機としての役割だけではない、そろばんの可能性を海外の方達だけではなく、日本においても皆さんに深く理解して頂き、
学校教育の現場で教具として活用してもらいたいとの考えについてお話させて頂きます。
Ø 申込方法: イベント管理アプリ“Peatix”のイベント公開ページから正会員もしくは非会員のチケットをお申し込みください
Peatix: < https://peatix.com/event/2713880/view >
Ø 応募締切: 9月7日(火)まで
◆講演会はZoom中継で開催します
◆講演会を聴講するためのZoomのURL、ミーティングID、パスコードは、
参加が確定された方に2021年9月8日(水)午後にメールでご連絡いたします
第20回総会が2021年5月30日に行われました。
今回もZoomを利用したオンライン・リモート開催でした。
2020年度事業活動報告、同収支決算、同じく2021年度事業活動計画、および同収支予算、
そして今期(2021年4月1日~)の監事の退任/就任について慎重にご審議頂き、
無事原案どおり、全て承認されましたのでご報告いたします。
第20回総会議事録報告書.pdf
第20回総会および講演会を開催いたします
今年もオンラインミーティングアプリ「Zoom」を使って開催することになりました。
ご都合により、ご参加できない場合には、「委任状」のご提出をお願いいたします。
※ 5月24日(月)までにFAX、E-Mailまたは郵便により事務局宛にお願いいたします。
日 時 : 2021年5月30日(日)
理事会 午後12時00分 ~ 午後12時30分
総 会 午後 1時00分 ~ 午後 1時30分
特別講演会 午後 1時40分 ~ 午後 3時00分
総会 議題 :
(1)2020年度事業活動報告および同収支決算について
(2)2021年度事業活動計画(案)および同収支予算(案)について
(3)その他
総会と講演会に参加するためのZoomミーティングの①URL、②ミーティングID、③パスワードは、メールでご連絡いたします。
つきましては、日本数学協会事務局まで参加申込みのメールを送信してください。
<総会・特別講演会に参加のためのメールは以下のようにしてください>
Ø あて先:sugakubunka@gmail.com
Ø 件名: 総会の参加について
Ø 本文: 氏名と電話番号だけは必ず記載してください
※送信いただいたメールアドレスに上記①~③のZoomの情報を5月28日までに発信いたします。
総会終了後に講演会を開催いたします。
特別講演会 :
『算額文化地理学のすすめ』
小川 束 氏(四日市大学)
< 講演会参加費 >
正会員:無料 (正会員の方は総会参加の要領でお申込みください)
非会員:1,000円 (非会員の方は Peatix からお申込みください)
Peatix:<https://peatix.com/ >
※PeatixをGoogle Chrome で開いた後、イベント検索で探してください
URL、IDとパスコードは、参加が確定された方に、メールで連絡します
※ 是非ご参加いただき、今後の活発な活動にご協力をお願いいたします。
日本数学協会の上野会長が下記のとおり
NHKカルチャー講座にて講義を行います。
【オンライン】代数幾何学への誘い
NHKカルチャーの横浜ランドマーク教室の主催
* 日時: 2021年2月6日(土) 15時30分~17時00分
* 講師: 四日市数学研究所所長・京都大学名誉教授 上野 健爾
代数幾何学は方程式で定義された図形の幾何学として出発し、数学の多くの分野の成果を取り入れて発展し続けている。
高校で学ぶ楕円、双曲線や放物線の自然な拡張である平面3次曲線は、楕円曲線とも呼ばれ、簡単な図形のようで奥深い性質を持っていて、今なお盛んに研究が続けられている。
また、楕円曲線の研究は暗号理論への応用とも結びついていて、代数幾何学の面白さを味わうことのできる研究対象である。
本講義では、楕円曲線を主題にして、代数・幾何・解析が興味深く絡み合う代数幾何学研究の現場に案内したい。
詳しくは、下記NHKカルチャーのサイトをご覧ください。
https://www.nhk-cul.co.jp/programs/program_1218155.html
2021年新春特別講義「ラマヌジャンと宇宙」が
2021年1月9日、10日にZoom中継で開催されました。
当日参加できなかった会員様、また、もう一度ゆっくり確認したい会員様のために、講義プログラムの中から3つ、その資料をご紹介いたします。
ログイン後、左側のページメニューに現れるグループスペースの“特別講義-講義資料”ページを開いていただき、
貼り付けしてあるそれぞれのpdfファイル名をクリックしていただくとご覧いただけます。
※会員限定ですので、資料をWEBなどで公開したり、拡散なさらないようお願いいたします。
1月9日(土)の実施分から
「ラマヌジャンの数学」 清水勇二氏(国際基督教大学教養学部教授)
「ラマヌジャン予想とゼータ関数」 高瀬幸一氏(宮城教育大学教育学部教授)
1月10日(日)の実施分から
「ロジャース=ラマヌジャン恒等式と表現論」 土岡俊介氏(東京工業大学情報理工学院講師)
第19回総会が2020年10月4日に行われました。
今回はZoomを利用したオンラインリモート開催でした。
2019年度事業活動報告、同収支決算、同じく2020年度事業活動計画、および同収支予算、
そして次期(2021年4月1日~)役員の選出について慎重にご審議頂き、
無事原案どおり、全て承認されましたのでご報告いたします。
第19回総会議事録報告書.pdf
2021年新春特別講義
現代数学・物理学入門講座
日本数学協会、四日市大学関孝和数学研究所、東京大学素粒子物理国際研究センター(ICEPP)の共催により新春特別講義を下記のように開催します。
新春特別講義「ラマヌジャンと宇宙」 (Zoom中継で開催)
* 日時: 2021年1月9日(土) 〜10日(日)
* 場所: Zoom中継で開催します
IDとパスコードは申し込みされた方に2021年1月5日頃にメールで連絡する予定です。
* プログラム:
1月 9日(土)
13:10~14:30 「ラマヌジャンの数学」 清水勇二氏(国際基督教大学教養学部教授)
14:45~16:45 「ラマヌジャン予想とゼータ関数」 高瀬幸一氏(宮城教育大学教育学部教授)
1月10日(日)
9:45~11:45 「ロジャース=ラマヌジャン恒等式と表現論」 土岡俊介氏(東京工業大学情報理工学院講師)
13:00~15:00 「モックテータ関数」 樋上和弘氏(九州大学数理学研究院准教授)
15:10~17:10 「対称性と宇宙のはじまり」 浅井祥仁氏(東京大学大学院理学系研究科教授)
* 受講料: 無料
* 参加資格:どなたでも参加できます(一部日程での参加も可)
* 募集人員:約150名(先着順)
* 応募方法:次の参加登録サイトにアクセスして住所・氏名・学校名(学生の場合は学年も)
または勤務先/所属先・メールアドレス・電話番号を入力して下さい。
https://forms.gle/783B8iGJpjaZSEvSA
12月25日(金)まで。(先着順受付)
申し込み後、2021年1月5日頃に Zoomの IDとパスコードをメールで送信します。
* 問合わせ先:新春特別講義事務局
メール:shinshun.jma@gmail.com
* 共催 : 日本数学協会・東京大学素粒子物理国際研究センター・四日市大学関孝和数学研究所
第19回総会および第18回年次大会(講演)を開催いたします。
※新型コロナが蔓延している現状では総会および年次大会を通常どおり開催することは難しいと考えますので、
今年はオンラインミーティングアプリ「Zoom」を使って開催することになりました。
総会と年次大会に参加するための①ZoomミーティングのURL、②ミーティングID、③パスワードは、
メールでご連絡いたします。つきましては、日本数学協会事務局まで参加申込みのメールを送信してください。
(当案内の下部に記載のメール方法のお願いをご覧ください。)
日 時 : 2020年10月4日(日)
理事会 午後12時30分 ~ 午後 1時00分
総 会 午後 1時00分 ~ 午後 1時30分
年次大会 午後 1時30分 ~ 午後 3時00分(予定)
総会 議題 :
(1)2019年度事業活動報告および同収支決算について
(2)2020年度事業活動計画(案)および同収支予算(案)について
(3)その他
※ご都合により、ご参加できない場合には、「委任状」に所要事項をご記入のうえ、
9月7日(月)までにFAXまたはE-Mail、郵便により事務局宛にご連絡くださいますようお願いいたします。
年次大会 WEB講演 :
『吉田光由と細川忠利』
後藤 典子氏(熊本大学永青文庫研究センター研究員)
上野 健爾氏(四日市大学 関孝和数学研究所)
是非ご参加いただき、今後の活発な活動にご協力をお願いいたします。
<総会・年次大会に参加のためのメールは以下のようにしてください>
Ø あて先:sugakubunka@gmail.com
Ø 件名: 総会・年次大会の参加について
Ø 本文: 氏名と電話番号だけは必ず記載してください
※送信いただいたメールアドレスに上記①~③のZoomの情報を9月下旬に発信いたします。
<本件担当> 日本数学協会 事務局
〒160-0011 東京都新宿区若葉1-10
TEL:03-6821-3313 FAX:03-5269-8182
E-Mail:sugakubunka@gmail.com
年次大会について
2020年(第18回)の年次大会を10月4日(日)に開催いたします。
オンライン会議アプリZoomで開きたいと思います。
詳しくは、会員の皆様に後日ご連絡いたします。
総会について
新型コロナウイルスの関係で5月予定の総会は延期します。
新しい日程は後日お知らせします。
会長 上野 健爾
日本数学協会・国際教育学会共催数学講座
2020年3月7日に予定していた下記の講座は延期することにな
新たな日時については後日に改めて掲示します。(
「数学活用の教科書を読む<第44回>」
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第44回>」
● 講師 宮永望、水谷一 (上野健爾、有田八州穂)
● 日時 2020年3月7日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編) 『数学活用』 新興出版社啓林館
・ この読書会は、テキストやその関連事項についての勉強会です。
・ テキストと無関係な数学の質問や発表は、お断りしております。
・ <第44回>に参加なさる方は、事前に世話人までご連絡ください。
(講師の個人アドレスでなく、下記のアドレスへお願いいたします。)
・ 事前の連絡がなくても参加可能ですが、
座席や資料の数に限りがありますので、予めご了承ください。
・ <第44回>にはテキストの
「日本人と数学」(122ページから)
の単元を読む予定です。
・ テキストは、高校数学の検定教科書ですが、
どなたでも(高校の生徒や教員でなくても)教科書販売店で購入可能です。
・ テキストをお持ちにならなくても参加可能ですが、
テキストをお持ちになることを前提にして読書会を進めます。
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
2020年新春特別講義 *** 全プログラム決定!! ***
現代数学・物理学入門
日本数学協会、 東京大学素粒子物理国際研究センター、四日市大学関孝和数学研究所の共催により
新春特別講義を下記のように開催します。
* 日時: 2020年1月11日(土) 〜12日(日)
* 場所: 東京大学小柴ホール(本郷キャンパス理学部1号館)
( http://www.u-tokyo.ac.jp/campusmap/cam01_00_25_j.html)
* プログラム:
1月11日(土) 受付12:30
13:00~14:30 「テータ関数から見えてくる数学」上野健爾氏(四日市大学 関孝和数学研究所)
14:45~16:45 「固有値問題からみた20世紀数学」黒川信重氏(東京工業大学名誉教授)
1月12日(日)
9:45~11:45 「層をめぐって」清水勇二氏(国際基督教大学 教養学部教授)
13:00~14:30 「量子力学から素粒子論へ」小林富雄氏(東京大学名誉教授)
14:45~16:45 「量子計算の枠組み」鈴木泰成氏(NTTセキュアプラットフォーム研究所 研究員)
* 受講料: 学生(含む大学生)無料 社会人1000円
* 参加資格:どなたでも参加できます(部分参加も可)
* 募集人員:約150名(先着順)
* 応募方法:往復はがきに住所、氏名、学校名(学生の場合は学年も)または勤務先および電話番号明記の上、
返信はがきに自分のあて先を書いて下記までお送りください。
12月25日(水)までに必着。(先着順受付)
〒182‐0025 調布市多摩川2-28-2コンデュ調布B-102号
四日市大学関孝和数学研究所東京分室
新春特別講義係
* 問合わせ先:四日市大学関孝和数学研究所東京分室 TEL042-444-5270
(宿泊の世話はできかねますのでご了承ください)
* 共催 : 日本数学協会・東京大学素粒子物理国際研究センター・四日市大学関孝和数学研究所
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第43回>」
● 講師 宮永望、水谷一 (上野健爾、有田八州穂)
● 日時 2019年11月23日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編) 『数学活用』 新興出版社啓林館
・ この読書会は、テキストやその関連事項についての勉強会です。
・ テキストと無関係な数学の質問や発表は、お断りしております。
・ <第43回>に参加なさる方は、事前に世話人までご連絡ください。
(講師の個人アドレスでなく、下記のアドレスへお願いいたします。)
・ 事前の連絡がなくても参加可能ですが、
座席や資料の数に限りがありますので、予めご了承ください。
・ <第43回>にはテキストの
「ハノイの塔を解く」(114ページから)、「データを予測する」(118ページから)
の単元を読む予定です。
・ テキストは、高校数学の検定教科書ですが、
どなたでも(高校の生徒や教員でなくても)教科書販売店で購入可能です。
・ テキストをお持ちにならなくても参加可能ですが、
テキストをお持ちになることを前提にして読書会を進めます。
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第42回>」
● 講師 宮永望、水谷一 (上野健爾、有田八州穂)
● 日時 2019年10月26日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編) 『数学活用』 新興出版社啓林館
・ この読書会は、テキストやその関連事項についての勉強会です。
・ テキストと無関係な数学の質問や発表は、お断りしております。
・ <第42回>に参加なさる方は、事前に世話人までご連絡ください。
(講師の個人アドレスでなく、下記のアドレスへお願いいたします。)
・ 事前の連絡がなくても参加可能ですが、
座席や資料の数に限りがありますので、予めご了承ください。
・ <第42回>にはテキストの
「パソコンで探る整数問題」(112ページから)、「ハノイの塔を解く」(114ページから)
の単元を読む予定です。
・ テキストは、高校数学の検定教科書ですが、
どなたでも(高校の生徒や教員でなくても)教科書販売店で購入可能です。
・ テキストをお持ちにならなくても参加可能ですが、
テキストをお持ちになることを前提にして読書会を進めます。
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第41回>」
● 講師 宮永望、水谷一 (上野健爾、有田八州穂)
● 日時 2019年9月28日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編) 『数学活用』 新興出版社啓林館
・ この読書会は、テキストやその関連事項についての勉強会です。
・ テキストと無関係な数学の質問や発表は、お断りしております。
・ <第41回>に参加なさる方は、事前に世話人までご連絡ください。
(講師の個人アドレスでなく、下記のアドレスへお願いいたします。)
・ 事前の連絡がなくても参加可能ですが、
座席や資料の数に限りがありますので、予めご了承ください。
・ <第41回>にはテキストの
「素数ゼミと暗号」(108ページから)、「パソコンで探る整数問題」(112ページから)
の単元を読む予定です。
・ テキストは、高校数学の検定教科書ですが、
どなたでも(高校の生徒や教員でなくても)教科書販売店で購入可能です。
・ テキストをお持ちにならなくても参加可能ですが、
テキストをお持ちになることを前提にして読書会を進めます。
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第40回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2019年8月31日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編) 『数学活用』 新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第40回>に参加なさるかたは,事前に世話人までご連絡ください.
(講師の個人アドレスでなく,下記のアドレスへお願いいたします).
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第40回>にはテキストの
「バーコードの秘密」(106ページから),「素数ゼミと暗号」(108ページから)
の単元を読む予定です.
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)教科書販売店で購入可能です.
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます.
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
第17回年次大会の開催のご案内
・ 場 所: 東京大学数理科学研究科棟(駒場) 講義室117・123
(京王井の頭線「駒場東大前」駅下車)
・ 参加費: 会員1,000円、 非会員2,000円 (但し、高校生以下の方は無料)
<午前の部>
*** 特別記念講演 ***
10:00~12:00 「つるさんかめさん~ニッポン算額探訪」 鑑賞
小寺 裕氏 (日本数学史学会運営委員)
<昼休み>ポスターセッション 12:00~13:30
<午後の部>
*** ワークショップ ***
1回目 13:30~14:30 2回目 15:00~16:00
※下記の両ワークショップを、同じ内容で2回づつ開催いたします。
① 「数学デッサン教室~正多面体のデッサンを体験する」 瑞慶山 香佳氏(数学画家)
瑞慶山(ずけやま)氏は数学や宇宙をテーマにしたデッサンの作品を数多く制作なさっており、数学や科学の展覧会に出典したりなさっています。
映画『センセイ君主』の装飾や今年度の『数学セミナー』誌の表紙にも協力なさっています。
瑞慶山氏は今年の1月に『数学デッサン教室』(技術評論社)を出版なさいましたが、今年の年次大会ではそのご著書のダイジェスト版のようなワークショップをしていただく予定です。
デッサンの初歩から「数学デッサン」の作品制作までを体験できる濃密な1時間となるはずです。
※各回申し込み順で15名程度までです。(参加は原則1人1回まで)
参加申し込み受付けは、当日の昼休みに行います。
※材料代としてワークショップ参加費が、1人500円になります。
(年次大会参加費とは別にいただきます)
② 「そろばんでやらない計算練習」 有田 八州穂氏(日本数学協会 幹事)
そろばんは与えられた問題を速く、正確にやることを目当てとします。
算数ではちょっと違います。物事を見て、問題を発見し、問題を設定し、解決する方法を自力で見つけ出すのが算数です。
そのようなそろばんとはちょっと違う計算練習をいっしょに話し合いながらやります。
《ポスターセッションのお申込みについて》
「ポスターセッション申込書」及び、「ポスターセッション予稿フォーム」につきましては、下記より印刷をしてください。
ポスターセッション申込書(2019年).docxポスターセッション予稿フォーム(2019年).docx
第18回総会が大東文化会館ホールにて、2019年5月19日に行われました。
2018年度事業活動報告、同収支決算、同じく2019年度事業活動計画、および同収支予算について
慎重にご審議頂き、無事原案通り、全て承認されましたのでご報告いたします。
第18回総会議事録報告書.pdf
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第39回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2019年7月6日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第39回>に参加なさるかたは,事前に世話人までご連絡ください.
(講師の個人アドレスでなく,下記のアドレスへお願いいたします).
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第39回>にはテキストの
「曲線を探す」(102ページから),「カーナビの秘密」(104ページから)
の単元を読む予定です.
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)教科書販売店で購入可能です.
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます.
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
第18回総会および特別講演会を開催いたします。
日 時 : 2019年5月19日(日)
理事会 午前11時30分 ~ 午後12時00分
総 会 午後12時00分 ~ 午後12時30分
特別講演会 午後 1時30分 ~ 午後 4時00分(予定)
※総会受付開始 午前11時15分~
会 場 : 大東文化会館ホール(東京都板橋区徳丸2-4-21)
(東武東上線「東武練馬駅」下車)
議 題 :
(1)2018年度事業活動報告および同収支決算について
(2)2019年度事業活動計画(案)および同収支予算(案)について
(3)その他
持ち物 : 第18回総会資料
ご都合により、ご出席できない場合には「委任状」のご提出をお願いいたします。
(5月13日(月)までにFAXまたはE-Mail、郵便により事務局宛にご連絡ください)
総会終了後に講演会を開催いたします。
≪ 特別講演について ≫
(1) 『数学活用の読書会の話題より』
宮永 望氏 (大学講師・日本数学協会幹事)
(2) 『そろばんを取り入れた算数』
田村 聡子氏 (大阪市公立小学校教諭)
講演会参加費: 正会員:無料
非会員:1,000円
是非ご参加いただき、今後の活発な活動にご協力をお願いいたします。
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第38回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2019年4月27日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第38回>に参加なさるかたは,事前に世話人までご連絡くださ
(講師の個人アドレスでなく,下記のアドレスへお願いいたします
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第38回>にはテキストの
「曲線を探す」(102ページから)
の単元を読む予定です.
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)教科書販売店で購入可
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます.
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第37回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2019年3月30日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第37回>に参加なさるかたは,事前に世話人までご連絡くださ
(講師の個人アドレスでなく,下記のアドレスへお願いいたします
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第37回>にはテキストの
「数式処理システムを使ってみよう」(98ページから)
の単元を読む予定です.
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)教科書販売店で購入可
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます.
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第36回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2019年2月16日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第36回>に参加なさるかたは,事前に世話人までご連絡くださ
(講師の個人アドレスでなく,下記のアドレスへお願いいたします
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第36回>にはテキストの
「数理シミュレーション」(94ページから)
の単元を読む予定です.
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)教科書販売店で購入可
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます.
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第35回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2018年1月26日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第35回>に参加なさるかたは,事前に世話人までご連絡くださ
(講師の個人アドレスでなく,下記のアドレスへお願いいたします
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第35回>にはテキストの
「正多面体を作る」(92ページから)
の単元を読む予定です(第32~34回と同様).
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)教科書販売店で購入可
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます。
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
「数学活用の教科書を読む」世話人(日本数学協会幹事) 宮永望
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第34回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2018年12月22日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第34回>に参加なさるかたは,
(講師の個人アドレスでなく,
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第34回>にはテキストの
「正多面体を作る」(92ページから)
の単元を読む予定です(第33回,第34回の続きです).
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます。
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第33回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2018年11月24日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第33回>に参加なさるかたは,事前に世話人までご連絡くださ
(講師の個人アドレスでなく,下記のアドレスへお願いいたします
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第33回>にはテキストの
「正多面体を作る」(92ページから)
の単元を読む予定です.
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)教科書販売店で購入可
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます。
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
高校生と社会人のための現代数学・物理学入門講座
新春特別講義
日本数学協会、東京大学素粒子物理国際研究センター、四日市大学関孝和数学研究所の共催により新春特別講義
「方程式を解く」
を下記のように開催しますのでご案内します。
日時 2019年1月12日(土) ~13日(日)
場所 東京大学小柴ホール(本郷キャンパス理学部1号館)
(http://www.u-tokyo.ac.jp/campusmap/cam01_00_25_j.html)
プログラム
1月12日(土) 受付13:15
13:45~15:00 「高次連立方程式を解く--関孝和の終結式の理論--」上野健爾(四日市大学 関孝和数学研究所)
15:15~16:45 「無限次方程式の解と応用--オイラーが考えたこと--」黒川信重(東京工業大学名誉教授)
1月13日(日)
9:30~11:00 「微分方程式を解く」 岡本 和夫(東京大学名誉教授)
11:15~12:45 「ワイエルシュトラスのペー関数と微分方程式」 清水勇二(国際基督教大学 教養学部教授)
14:30~16:30 「物理の方程式を解く」 小林富雄(東京大学名誉教授)
受講料:学生(含む大学生)無料 社会人1000円
参加資格:どなたでも参加できます(部分参加も可)
募集人員:約150名(先着順)
応募方法:往復はがきに住所、氏名、学校名(学生の場合は学年も)または勤務先および電話番号明記の上、
返信はがきに自分のあて先を書いて下記までお送りください。
12月25日までに必着のこと。(先着順受付)
〒160-0022 東京都新宿区新宿2-3-16
ライオンズマンション御苑前504号室
四日市大学関孝和数学研究所東京分室
新春特別講義係
* 問合わせ先:四日市大学関孝和数学研究所東京分室 TEL&Fax03-5925-8347
(宿泊の世話はできかねますのでご了承ください)
* 共催 : 日本数学協会・東京大学素粒子物理国際研究センター・四日市大学関孝和数学研究所
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第32回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2018年10月13日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第32回>に参加なさるかたは,事前に世話人までご連絡くださ
(講師の個人アドレスでなく,下記のアドレスへお願いいたします
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第32回>にはテキストの
「正多面体を作る」(92ページから)
の単元を読む予定です.
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)教科書販売店で購入可
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます。
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
****************
秋のイベントの日程が決まりました.
~「数楽カフェ in ふくしま」~
1.「お母さんのための-ほっとひといき-数楽カフェ」(10月
2.「高校生のための-はっとひらめく‐数学講座」(10月20
3.「映画『算法少女上』上映会」(10月20日)
4.「親子のための‐あっとおどろく‐サイエンス・
下記お知らせを掲載いたします。
ご参加をお待ちしております。

● 日時 : 2018年9月23日(日) 午前10時より
● 場所 : 東京大学数理科学研究科棟(駒場) 大講義室にて
(京王井の頭線「駒場東大前」駅下車)
《午前の部》
~特別記念講演~ 10:00~12:00
v 「算数で何を学ぶか」 黒木哲徳氏(前都城教育委員会教育長)
v 黒木氏・上野会長・藤井副会長・佐藤和孝氏・有田氏によるパネルディスカッション
テーマ「算数で何を学ぶか」 司会進行:岡本副会長
《昼休み》 ポスターセッション 12:00~13:30
《午後の部》
~ワークショップ~ 13:30~16:30
v「そろばんと算数・考える力をどうつけるか」 有田八州穂氏(日本数学協会 幹事)
現在「日本珠算」に連載中の「考える力をつける問題」の執筆者有田八州穂先生がそろばんと算数を、
どのように考える力に結び付けるかを、解説してくださいます。
v 「証明だけが数学じゃない ~事実の中に数学は潜んでいる」
矢崎成俊氏(明治大学 理工学部 教授)
矢崎氏は数学者として「移動境界問題の数理解析」の研究をなさっていますが、執筆や講演・ワークショップを
通して「実験数学」の普及活動もなさっています。簡単な工作や実験で遊んでいるうちに面白くて深い数学の世
界が体験できる、という玩具や教具を数多く開発なさっています。それらはご著書の『実験数学読本』や月刊誌
『数学セミナー』に連載中の記事でも紹介されていますが、この機会にご自身の目と手で体験なさいませんか。
―案内者 宮永氏―
この年次大会の参加料は、会員が1,000円、非会員が2,000円を予定しています(高校生以下の学生の方は無料です)。
《ポスターセッションのお申込みについて》
「ポスターセッション申込書」及び、「ポスターセッション予稿フォーム」につきましては、下記より印刷をしてください。
ポスターセッション申込書(2018年).docx
ポスターセッション予稿フォーム(2018年).docx
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第31回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2018年7月28日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室7号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第31回>に参加なさるかたは,
(講師の個人アドレスでなく,
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第31回>にはテキストの
「地球を測る[2]」(88ページから)
の単元を読む予定です.
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます。
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
西日本の大雨災害とのことですが,
第17回総会が大東文化会館ホールにて、平成30年5月27日に行われました。
平成29年度事業活動報告、同収支決算、同じく平成30年度事業活動計画、および同収支予算について慎重にご審議頂き、
無事原案通り、全て承認されましたのでご報告いたします。
総会議事録報告書.pdf
「三春まちなか寺子屋」の第2弾が今年度年4回の企画で実施されます.
下記お知らせを掲載いたします。
ご参加をお待ちしております。

日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第30回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2018年6月30日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室7号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第30回>に参加なさるかたは,
(講師の個人アドレスでなく,
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第30回>にはテキストの
「敷き詰めの問題」(82ページから),
「あなたの誕生日は何曜日?」(86ページから)
の単元を読む予定です.
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます。
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第29回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2018年5月26日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室7号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第29回>に参加なさるかたは,
(講師の個人アドレスでなく,
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第29回>にはテキストの
「音楽と数学」(78ページから),「敷き詰めの問題」(
の単元を読む予定です.
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます。
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
第17回総会および特別講演会を開催いたします。
日時 : 平成30年5月27日(日)
理事会 午前11時30分 ~ 午後12時00分
総 会 午後12時00分 ~ 午後12時30分
特別講演会 午後 1時30分 ~ 午後 4時00分(予定)
※総会受付開始 午前11時15分~
会場 : 大東文化会館ホール (東京都板橋区徳丸2-4-21)
(東武東上線 「東武練馬」駅 下車)
議題 :
① 平成29年度事業活動報告および同収支決算について
② 平成30年度事業活動計画(案)および同収支予算(案)につ他て
③ 次期(平成31年4月1日~平成33年3月31日)役員の選出について
④ その他
ご都合により、ご出席できない場合には、『委任状』のご提出をお願いいたします。委任状.pdf
(5月21日までにお願いいたします)
総会終了後に講演会を開催いたします。
《 特別講演について 》
(1) 『そろばんの歴史と文化』
太田 敏幸氏 (珠算史研究学会 会長)
(2) 『ほんとうはむずかしい算数』
有田 八州穂氏 (日本数学協会 幹事)
是非ご参加いただき、今後の活発な活動にご協力をお願いいたします。
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第28回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2018年4月28日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第28回>に参加なさるかたは,
(講師の個人アドレスでなく,
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第28回>に読むのはテキストの
「芸術と数学」(74ページから),「音楽と数学」(
の単元です.
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます。
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第27回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2018年3月31日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第27回>に参加なさるかたは,
(講師の個人アドレスでなく,
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第27回>はテキストの
「芸術と数学」(74ページ)
の単元から読み進めます.
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます。
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
今週2月23日金曜夜9時から、
読売テレビ開局60年スペシャルドラマ
「天才を育てた女房~世界が認めた数学者と妻の愛~」
というタイトルで日本テレビ・読売テレビ系で放送されます。
数学者岡潔さんご夫妻の実話をもとにしたドラマだそうです。
http://www.ytv.co.jp/tensai/
日本数学協会・国際教育学会の読書会は2012/6/
第1シリーズ(遠山啓『数学入門』
第2シリーズ(根上生也(編)『
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第26回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 特別講師 荒木義明
(日本テセレーションデザイン協会代表)
● 日時 2018年2月24日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第26回>に参加なさるかたは,
(講師の個人アドレスでなく,
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第26回>はテキストの
「芸術と数学」(74ページ)
の単元から読み進めます.
・ <第26回>が初参加でも,特に不都合はありません.
・ <第26回>は特別講師として荒木義明氏をお呼びします.
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます.
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第25回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2017年12月23日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室7号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第25回>に参加なさるかたは,
(講師の個人アドレスでなく,
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第25回>はテキストの
「芸術と数学」(74ページ)
の単元から読み進めます.
・ <第25回>が初参加でも,特に不都合はありません.
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます.
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
高校生と社会人のための現代数学・物理学入門講座
新春特別講義
日本数学協会、 東京大学素粒子物理国際研究センター、
四日市大学関孝和数学研究所の共催により新春特別講義
「オイラーの数学・物理学」
オイラーの基本的な業績の重要なものを数学者、物理学者がわかりやすく講義します。
* 日時 2018年1月6日(土) ・ 7日(日)
* 場所 東京大学小柴ホール<東京大学本郷キャンパス理学部1号館>
++++++ プログラム ++++++
1月6日(土) 受付 13:15
●13:45~15:00 「オイラーと複素数」
講師:上野健爾(四日市大学 関孝和数学研究所)
●15:15~16:45 「オイラーのゼータ関数をめぐって」
講師:黒川信重(東京工業大学 名誉教授)
1月7日(日)
●10:00~11:45 「多面体定理 : トポロジーの出発点」
講師:清水勇二(国際基督教大学 教養学部)
●13:30~15:30 「変分法と物理学」
講師:小林富雄(東京大学 名誉教授)
++++++++++++++++++++++++++++++++++++++++++++++++
* 受講料 : 学生(含む大学生) 無料 社会人1,000円
* 参加資格 : どなたでも参加できます(部分参加も可)
* 募集人数 : 約120名(先着順)
* 応募方法 : 往復はがきに住所、氏名、学校名(学生の場合は学年も)または勤務先および電話番号明記の上、
返信はがきに自分の宛先を書いて下記までお送りください。12月25日(月)までに必着のこと。(先着順受付)
〒160-0022 東京都新宿区新宿2-3-16 ライオンズマンション御苑前504号室
四日市大学関孝和数学研究所東京分室 新春特別講義係
* 問合わせ先:四日市大学関孝和数学研究所東京分室 TEL&Fax03-5925-8347
(宿泊の世話はできかねますのでご了承ください)
* 共催 : 日本数学協会・東京大学素粒子物理国際研究センター・四日市大学関孝和数学研究所
2018新春特別講義オイラーの数学・物理学.pdf
数学月間勉強会ー「結晶空間群で,物理と数学を学ぼう」第3回が近づきました.
日程が形の科学会と続きご迷惑おかけしますが,変更できませんので予定通り実施します.
御多忙な時期ですがどうぞご参加ください.
主催●日本数学協会,数学月間の会(SGK)
日時●12月12日,14:30-17:00
会場●東京大学出版会,会議室
線路沿いの留学生会館などのある敷地内の一番奥の建物です.
東大構内ではありませんからご注意ください.
最寄り駅●京王井の頭線「駒場東大前」
参加費●無料
問合せ・申し込み●sgktani@gmail.com,谷克彦
第3回テーマ●「結晶空間群の作り方」
数学月間勉強会の特徴は,物理と数学の両視点から数学誕生を理解
福島県田村郡三春町からのお知らせです。
日本数学協会 第15回年次大会で上映いたしました『算法少女』の
上映会もおこなわれるそうです。
ご都合のよろしい方は、ご参加してみてはいかがでしょうか。
和算で遊ぼう!
●三春町内神社仏閣の算額巡り&和算遊び手習い
日時● 第12回:平成29年12月9日(土) 10:30 ~ 12:00
第12回開催後、『算法少女』上映会を行います。
上映開始13:00~
詳細につきましては、下記サイトにてご確認をお願いいたします。
http://miharukoma.com/experience/856
http://miharukoma.com/event/4194
お問合せは、(株)三春まちづくり公社観光部/みはる観光協会 TEL:0247-62-3690 まで
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第24回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2017年11月11日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室7号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第24回>に参加なさるかたは,
(講師の個人アドレスでなく,
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第24回>はテキストの
「芸術と数学」(74ページ)
の単元から読み進めます.
・ <第24回>が初参加でも,特に不都合はありません.
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます.
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
Twitterをはじめました。
ユーザー名:日本数学協会
よろしくお願いいたします。
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第23回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2017年10月14日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室7号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第23回>に参加なさるかたは,
(講師の個人アドレスでなく,
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
・ <第23回>はテキストの
「無限とパラドックス」(70ページ)
の単元から読み進めます.
・ <第23回>が初参加でも,特に不都合はありません.
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます.
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
数学月間勉強会ー「結晶空間群で,物理と数学を学ぼう」第2回
主催●日本数学協会,数学月間の会(SGK)
日時●9月26日,14:30-17:00,(開場14:00)
会場●東京大学出版会,会議室
最寄り駅●京王井の頭線「駒場東大前」
参加費●無料
問合せ・申し込み●sgktani@gmail.com,谷克彦
第2回テーマ●「美しい多面体と点群,結晶点群の鑑賞」
第1回は周期的空間でした.第2回は有限図形の対称性を鑑賞し,
次回の周期的空間の対称性につなぎます.
数学月間勉強会の特徴は,物理と数学の両視点から数学誕生を理解
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第22回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2017年9月2日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます.
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第22回>はテキストの
「無限とパラドックス」(70ページ)
の単元から読み進めます.
・ <第22回>が初参加でも,特に不都合はありません.
・ <第22回>に参加なさるかたは,
(講師の個人アドレスでなく,
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
第15回年次大会を開催いたします
日時:9月23日(土) 午前10時より
場所:東京大学数理科学研究科棟(駒場) (京王井の頭線「駒場東大前」駅下車)
《午前の部》
~特別記念講演~ 10:00~12:00
『算法少女』上映会 を開催いたします。
原作者 遠藤 寛子氏 をお招きして、お話しをお伺いする予定でおります。
《ヤングセッション》 12:00~12:30
洛北高校 2年生 3名によるヤングセッションを予定しております。
《昼休み》 ポスターセッション 12:15~13:30
《午後の部》 ~ワークショップ~
v 「これからの算数教育(仮)」 13:30~15:00
大場 一輝氏(三鷹市立中原小学校 校長)
v 「数学的曲面が拓くジャグリングの世界」 15:15~16:45
松浦 昭洋氏(東京電機大学)
ワークショップ等の詳細は、日本数学協会のホームページに掲載をいたします。
ご確認をお願いいたします。
なお、年次大会参加費は会員1,000円、会員外2,000円 になります。
(但し、大学生、高校生および引率者の教師、父母も無料になっております)
皆様のご参加をお待ちしております。
※ポスターセッション 申込書 及び 予稿フォーム は下記より印刷ください。
ポスターセッション申込書(2017年).docx
ポスターセッション予稿フォーム(2017年).docx
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第21回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2017年8月5日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます.
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第21回>もテキストの
「数学者を悩ませた問題」(68ページ)
の単元から読み進めます.
・ <第21回>が初参加でも,特に不都合はありません.
・ <第21回>に参加なさるかたは,
(講師の個人アドレスでなく,
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
△▼△▼ 数学月間からのお知らせ△▼△▼
ICUオープンキャンパスでのモデル授業
題目:シンメトリー -- 不思議なタイル貼り
講師:清水勇二
日時:8月5日(土)11:05〜11:50、14:05〜
(同じ講義を2回します。)
場所:国際基督教大学 理学館2F 220 教室
(東京都三鷹市大沢 3-10-2)
△▼△ 数学月間の会からのお知らせ △▼△
数学月間の夏がやってまいりました.
今年の数学月間懇話会(7/22)は土曜日ですので,
多くの方のご参加を期待しております.
今年から,数学月間懇話会の他に
数学月間勉強会のシリーズをスタートしました.
最初のシリーズ(4回もの)は,私の趣味で恐縮ですが,
「結晶空間群で物理と数学を学ぼう」です.
こちらもご参加お勧めします.
ーーーー記ーーーーーー
■数学月間懇話会(第13回)
●日時:7月22日(土),13:50-17:20,開場:13
●場所:東京大学(駒場),数理科学研究科棟002号室
●参加費無料
直接会場にお出で下さい.
●主催:数学月間の会,日本数学協会
●問い合わせ:sgktani@gmail.com
●プログラム
1.社会調査の実際,森本栄一(ビデオリサーチ)
2.ブラックホールを見る,池田思朗(統数研)
3.星型正多面体の体積比較(模型も作るよ!),小梁修(osa
17:30から,学内のイタリアントマトで懇親会をします(飲食
■結晶空間群で物理と数学を学ぼう
第1回は●6月28日,15:00-17:00
会場●東京大学出版会,会議室
最寄り駅●京王井の頭線「駒場東大前」,駅から400m位歩きま
参加費●無料
問合せ・申し込み●sgktani@gmail.com,谷克彦
第1回テーマ●「周期と空間のデジタル化」,繰り返し模様を鑑賞
なお,このシリーズは4回の連続物の予定です.
第2回:結晶点群,第3回:並進群の拡大としての結晶空間群,第
数学月間勉強会の特徴は,物理と数学の両視点から数学誕生を理解
第16回総会が大東文化会館ホールにて、平成29年5月21日に行われました。
平成28年度事業活動報告、同収支決算、同じく平成29年度事業活動計画、および同収支予算について慎重にご審議頂き、
無事原案通り、全て承認されましたのでご報告いたします。
日本数学協会第16回総会議事録.pdf
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第20回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2017年5月27日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室7号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代と飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます.
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第20回>はテキストの
「数学者を悩ませた問題」(68ページ)
の単元から読み進めます.
・ <第20回>が初参加でも,特に不都合はありません.
・ <第20回>に参加なさるかたは,
(講師の個人アドレスでなく,
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
第16回総会および特別講演会を開催いたします。
日時 : 平成29年5月21日(日)
理事会 午前11時30分 ~ 午後12時00分
総 会 午後12時00分 ~ 午後12時30分
特別講演会 午後 1時30分 ~ 午後 4時00分(予定)
※総会受付開始 午前11時15分~
会場 : 大東文化会館ホール (東京都板橋区徳丸2-4-21)
(東武東上線 「東武練馬」駅 下車)
議題 :
① 平成28年度事業活動報告(案)および同収支決算(案)について
② 平成29年度事業活動計画(案)および同収支予算(案)について
③ その他
ご都合により、ご出席できない場合には、『委任状』のご提出をお願いいたします。
(5月15日までにお願いいたします)
総会終了後に講演会を開催いたします。
《 特別講演について 》
(1) 『算額との出会い』
八谷 園子氏 (四日市市立富田中学校)
(2) 『文化としての算額,教育としての算額』
小川 束氏 (四日市大学)
是非ご参加いただき、今後の活発な活動にご協力をお願いいたします。
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第19回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2017年4月22日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室7号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代+飲み物代(合計で1人あたり約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます.
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第19回>はテキストの
「数学者を悩ませた問題」(68ページ)
の単元から読み進めます.
・ <第19回>が初参加でも,特に不都合はありません.
・ <第19回>に参加なさるかたは,
(講師の個人アドレスでなく,
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第18回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2017年3月11日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室7号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代+飲み物代(=約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます.
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第18回>はテキストの
「分布を比較する」(58ページ)
の単元から読み進めます.
・ <第18回>が初参加でも,特に不都合はありません.
・ <第18回>に参加なさるかたは,
(講師の個人アドレスでなく,
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
日本数学協会・国際教育学会共催数学講座
「数学活用の教科書を読む<第17回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2016年12月10日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室7号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代+飲み物代(=約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます.
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第17回>はテキストの
「表計算ソフトウェアを使ってみよう」(56ページ)
の単元から読み進めます.
・ <第17回>が初参加でも,特に不都合はありません.
・ <第17回>に参加なさるかたは,
(講師の個人アドレスでなく,
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
***************
日本数学協会、 東京大学素粒子物理国際研究センター、
四日市大学関孝和数学研究所の共催により新春特別講義
を下記のように開催しますのでご案内します。
今回はこれまでの会場とはが異なりますのでご注意下さい。
* 日時 2017年1月7日(土) ・ 8日(日)
* 場所 東京大学内<ダイワユビキタ学術研究館>
ダイワハウス石橋信夫記念ホール(東大本郷キャンパス)
東京大学 [本郷キャンパスマップ(情報学環・ダイワユビキタス学術研究館)].pdf
++++++ プログラム ++++++
1月7日(土) 受付 13:15
●13:45~15:00 「複素数の微積分――オイラー・コーシー・リーマンが考えたこと」
講師:上野健爾(四日市大学 関孝和数学研究所)
●15:15~16:45 「リーマン面をめぐって」
講師:桂 利行(法政大学 理工学部経営システム工学科)
1月8日(日)
●10:00~11:45 「リーマンから始まる幾何学」
講師:清水勇二(国際基督教大学 教養学部)
●13:30~15:30 「リーマンから始まる物理学」
講師:小林富雄(東京大学 名誉教授)
++++++++++++++++++++++++++++++++++++++++++++++++
* 受講料 : 学生(含む大学生) 無料 社会人1,000円
* 参加資格 : どなたでも参加できます(部分参加も可)
* 募集人数 : 約120名(先着順)
返信はがきに自分の宛先を書いて下記までお送りください。12月25日までに必着のこと。(先着順受付)
〒160-0022 東京都新宿区新宿2-3-16 ライオンズマンション御苑前504号室
四日市大学関孝和数学研究所東京分室 新春特別講義係
* 問合わせ先:四日市大学関孝和数学研究所東京分室 TEL&Fax03-5925-8347
(宿泊の世話はできかねますのでご了承ください)
* 共催 : 日本数学協会・東京大学素粒子物理国際研究センター・四日市大学関孝和数学研究所2017年新春特別講義リーマンちらし.pdf
福島県田村郡三春町からのお知らせです
ご都合のよろしい方は、ご参加してみてはいかがでしょうか。
和算で遊ぼう!
●三春まちなか寺子屋
日時●平成29年1月~12月
毎月1回開催(第2土曜日)10:00~(2時間程度)
第1回:平成29年1月14日(土)
内容●町内神社仏閣の算額巡り+和算遊び手習い
場所●福島県田村郡三春町大字西方字石畑270-1
自然観察ステーション(駐車場:三春の里田園生活館)
講師●五輪教一
参加費●大人10,000円/12回分、高校生以下3,000円/12回分
※空きがある場合、大人1,000円/1回、高校生以下300円/1回
申込み・問合せ先●㈱三春まちづくり公社/観光部 0247-62-3690
日本数学協会・国際教育学会共催数学講座(読書会)
「数学活用の教科書を読む<16回>」
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
● 日時 2016年10月29日(土) 15:00~17:00
(会場は14:30~17:30を押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下6階)
● 会費 3時間分の会場代+飲み物代(=約1000円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
・ 時間が前回とは異なりますのでご注意ください(前々回までと同じ時間です).
・ 会場が前々回までとは異なりますのでご注意ください(前回と同じ会場です).
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)教科書販売店で購入可能です.
・ テキストをお持ちにならなくても参加可能ですが,
テキストをお持ちになることを前提にして読書会を進めます.
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問や発表は,お断りしております.
・ <第16回>はテキストの
「どうやって議席が決まるのか」(54ページ)
の単元から読み進めます.
・ <第16回>が初参加でも,特に不都合はありません.
・ <第16回>に参加なさるかたは,事前に世話人までご連絡ください.
(講師の個人アドレスでなく,下記のアドレスへお願いいたします).
・ 事前の連絡がなくても参加可能ですが,
座席や資料の数に限りがありますので,予めご了承ください.
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
(重要)サーバー移転に伴うメンテナンスのお知らせ
2016年9月14日12:00よりサーバー移転作業を行います。
それに伴い、24時間から48時間程度の間、数学文化協会サイトへのアクセスができません。
ご不便をおかけしますが、何卒ご理解のほどよろしくお願い申し上げます。
(9月14日14:15追記)
メンテナンス作業は終了しました。こちらの追記メッセージが表示されている場合は問題なくサイトがご利用いただけます。
ご協力ありがとうございました。
日本数学協会・国際教育学会共催数学講座(読書会)
「数学活用の教科書を読む<15回>」
● 日時 2016年10月08日(土) 13:00~15:00
(会場は12:30~15:30まで押さえてあります)
● 会場 喫茶室ルノアール 新宿3丁目ビッグスビル店 貸会議室6号室
(東京都新宿区新宿2-19-1 ビッグスビル地下2階)
● 会費 3時間分の会場代(=(2160円×3-補助金)÷人数)
+飲み物代(≧590円)
● テキスト 根上生也(編)『数学活用』新興出版社啓林館
● 講師 宮永望,水谷一 (上野健爾,有田八州穂)
・ <第14回>までとは時間も会場も異なりますのでご注意ください.
・ <第16回>からの時間や会場は未定です.
・ テキストは,高校数学の検定教科書ですが,
どなたでも(高校の生徒や教員でなくても)教科書販売店で購入可能です.
・ できるだけテキストを持参してご参加ください.
・ この読書会は,テキストやその関連事項についての勉強会です.
・ テキストと無関係な数学の質問・発表は,受け付けておりません.
・ <第15回>はテキストの
「新聞に現れる数値」(52ページ)
の単元から読み進めます.
・ <第15回>が初参加でも,特に不都合はありません.
・ 日本数学協会・国際教育学会共催の勉強会に初めて参加なさる方は,
つぎのメールアドレスへ氏名・メールアドレスをご連絡ください
(ご連絡いただいた氏名・メールアドレスは,
勉強会の事務的な目的以外では使用いたしません).
● 「数学活用の教科書を読む」世話人 suugakukatuyou@gmail.com
第14回年次大会 特別記念講演 資料について
第14回年次大会 特別記念講演で配付しました資料のデータは下記になります。
当日、お手元に資料が渡らなかった会員様には、大変ご迷惑をおかけいたしました。
お詫び申し上げます。
日本数学協会講演(2016年9月11日).pdf
委任状のお願い
9月11日(日)に開催されます、臨時総会につきまして、委任状を送付くださいました
会員の皆様、ありがとうございました。
当日ご出席できない会員の方で、まだ「委任状」を送付されていない方は、所要事項をご記入のうえ、
FAXまたはE-Mail、郵便により事務局宛に至急ご連絡をくださいますよう何卒よろしくお願いいたします。
臨時総会(委任状).pdf
国際教育学会の事務局より下記のようなお知らせを頂戴致しました。
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
国際教育学会(ISE)会員、顧問、関係者の皆様
すでに出欠のお返事をいただいている方にもご案内しておりますが、何卒ご容赦ください。
国際教育学会 第11回大会公開シンポジウム「教育を科学する」の御案内を再送させていただきます。
ご多忙のところ誠に恐縮でございますが、ご都合よろしければご参加いただけますと幸いです。
【国際教育学会第11回年次大会プログラム】
日 時:2016年9月3日(土)12:20~18:15
会 場:京都大学百周年時計台記念館国際交流ホールI
【プログラム】※シンポジウムの詳細は添付のプログラムをご覧ください。
12:20~12:40 国際教育学会総会
12:45~13:45 公開シンポジウム第一部
13:45~14:50 公開シンポジウム第二部
14:50~18:15 公開シンポジウム第三部
18:20~ 懇親会(懇親会費3,000円)
※懇親会の会場は京都大学百周年時計台記念館会議室Ⅲとなっております。
【アクセス】
・会場とアクセス:会場となります京都大学百周年時計台記念館国際交流ホールIは、京都大学吉田キャンパスの本部構内にございます。
・京都大学吉田キャンパスへのアクセス:
http://www.kyoto-u.ac.jp/ja/access/campus/
・吉田キャンパスの構内配置図:
http://www.kyoto-u.ac.jp/ja/access/campus/map5r.htm
・吉田キャンパス本部構内マップおよび主な交通機関からのアクセス:
http://www.kyoto-u.ac.jp/ja/access/campus/map6r_y.htm
百周年時計台記念館は3番の建物です。国際交流ホールIはその2階にございます。
・最寄りの駅:京阪本線「出町柳」駅から東へ徒歩15分
または京都市営バス「京大正門前」下車(路線によっては「百万遍」で下車ください。)
出欠のご連絡をされておられない方は、以下の書式に☑を記入の上ご返信ください。
--------------------------------書式--------------------------------
国際教育学会(ISE) 事務局 行
E-mail: ise@sfi-npo.net
FAX: 075-753-7157
・国際教育学会総会(平成28年9月3日 12:20~12:40)
□出席 □欠席
・公開シンポジウム「教育を科学する」(平成28年9月3日 12:45~18:15)
□出席 □欠席
・懇親会(平成28年9月3日 シンポジウム終了後)
□出席 □欠席
会場: 京都大学時計台記念館会議室Ⅲ
参加費:3000円
なお、総会ご欠席の場合は、必ず下記の委任状に氏名をご記入の上、ご返信・返送ください。
--------------------------------------------------------------------
委 任 状
平成28年9月3日に開催される第11回国際教育学会(ISE)における議決を、
会長へ委任いたします。
平成 28年 月 日
氏名
--------------------------------------------------------------------
****************************************************
国際教育学会(ISE) 事務局
〒606-8501
京都市左京区吉田本町 京都大学経済研究所内
Tel: 075-753-7184
E-mail: ise@sfi-npo.net
Homepage: http://sfi-npo.net/ise/
****************************************************
場所: 東京大学数理科学研究科棟(駒場) (京王井の頭線「駒場東大前」)
<午前の部>
*** 特別記念講演 ***
10:00~11:30 「パリのライプニッツ」 (仮題)
林 知宏氏 (学習院高等科)
*** 臨時総会 ***
11:30~12:00 議題 : ① 平成29年度以降の役員選出について
② 正会員年会費の値上げについて
<昼休み>ポスターセッション 12:00~13:15
<午後の部>
*** ワークショップ ***
① 13:15~14:15 「珠算をとりいれた算数教科書「そろばんで さんすう」の作成について」
田村 聡子氏(大阪市立開平小学校教諭)
② 14:30~16:30 「オリンピックエンブレムの数理とその展開」
荒木 義明氏(日本テセレーションデザイン協会(代表))
※当日は、はさみとセロハンテープ(透明のもの)をご持参ください。
ワークショップで使用いたします。
なお、参加料は、会員が1,000円、非会員が2,000円になります。
(但し、大学生、高校生および引率者の教師、父母も無料になっています)。
準備の都合上、ご参加ご希望の方は、メールまたはファックス、郵送にて事前に事務局宛にご連絡をお願い申し上げます。
【本件担当】 日本数学協会 事務局
〒160-0011 東京都新宿区若葉1-10
℡: 03-6821-3313 FAX: 03-5269-8182
E-Mail: sugakubunka@gmail.com
会員の皆様には、益々ご清祥のこととお慶び申し上げます。
この度、東北大学 高度教養教育・学生支援機構 の主催により、
数理科学教育シンポジウム「市民的教養としての数理科学 -大学教育で数量的リテラシーを育てる-」
が開催されますので、ご案内いたします。
数理科学教育シンポジウム
「市民的教養としての数理科学 -大学教育で数量的リテラシーを育てる-」
日時:2016年9月9日(金) 13:00-17:30
場所:TKP東京駅日本橋カンファレンスセンターホール5B
その他、詳細は以下のWebを御覧ください。
・ポスター: https://www.ihe.tohoku.ac.jp/pd/files/1469416308.pdf
・詳細・申込み: https://www.ihe.tohoku.ac.jp/pd/index.cgi?program_num=1467600912
皆様奮ってご参加くださいますよう、心よりお願い申し上げます。
~ お知らせ ~
下記の通り、セミナーおよび研究集会が開催されます。
ご都合のよろしい方は、是非ご参加ください。
● 日本フィボナッチ協会/第14回研究集会
日 時 2016年8月26日(金曜日) 10時00分~17時30分
場 所 東京理科大学(神楽坂キャンパス)2号館4階の241・242教
アクセス 飯田橋駅(JR総武線、東京メトロ 東西線、有楽町線、南北線、都営大江戸線)徒歩5分
参 加 費 1000円(中学生・高校生・高専生は無料)
主催:日本フィボナッチ協会
協賛:東京理科大学理数教育研究センター
●街角の数学「第2回夏季セミナー」
(添付pdf資料の通りです
街角の数学お知らせ.pdf
第15回総会が大東文化会館ホールにて、平成28年5月22日に行われました。
平成27年度事業活動報告、同収支決算、同じく平成28年度事業活動計画、および同収支予算について慎重にご審議頂き、
無事原案通り、全て承認されましたのでご報告いたします。
第15回総会議事録.pdf
「数学活用の教科書を読む<13回目><14回目>
● 日時: 13回目・・2016年7月2日(土) 15:00~17:00
● 会場:両日とも,正進社 5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 編集部伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講師: 宮永 望,水谷 一,(上野健爾,有田八州穂)
● 講座内容:
*高校教科書「数学活用」の話題をもとに,
*多方面に活用されている数学では,
奇心満載で学べます。
(例)数と計算の進化,新しい幾何学,優勝チームの決め方,
音楽と数学,素数ゼミと暗号,世界のゲーム・パズル,
*前回の講座に参加していなくても,
*小・中・高校の先生には,単元導入時の話題提供や児童・
にぴったりです。
● 講座詳細:
*毎回1/2~1単元ほど読み進めます。
*7月講座では,
*講師の先生から,
● 使用教材:
*新興出版社 啓林館発行 高校教科書 「数学活用」(550円)
● 会場地図:下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/
◎ 正進社会場は,7月講座で終了となります。
「数学活用の教科書を読む<12回目>」
● 日時: 2016年6月4日(土) 15:00~17:00
● 会場: 正進社 5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講師: 宮永 望,水谷 一,(上野健爾,有田八州穂)
● 講座内容:
*高校教科書「数学活用」の話題をもとに,
*多方面に活用されている数学では,
(例)数と計算の進化,新しい幾何学,優勝チームの決め方,
音楽と数学,素数ゼミと暗号,世界のゲーム・パズル,
*前回の講座に参加していなくても,
*小・中・高校の先生には,単元導入時の話題提供や児童・
● 講座詳細:
*毎回1/2~1単元ほど読み進めます。
*6月講座では,「世界のゲーム・パズル」から読み進めます。
*講師の先生から,
● 使用教材:
*新興出版社 啓林館発行 高校教科書 「数学活用」(550円)
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/
「数学活用の教科書を読む<11回目>」
● 日時: 2016年4月23日(土) 15:00~17:00
● 会場: 正進社 5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講師: 宮永 望,水谷 一,(上野健爾,有田八州穂)
● 講座内容:
*高校教科書「数学活用」の話題をもとに,
*多方面に活用されている数学では,
(例)数と計算の進化,新しい幾何学,優勝チームの決め方,
音楽と数学,素数ゼミと暗号,世界のゲーム・パズル,
*前回の講座に参加していなくても,
*小・中・高校の先生には,単元導入時の話題提供や児童・
● 講座詳細:
*毎回1/2~1単元ほど読み進めます。
*4月講座では,「優勝チームの決め方」から読み進めます。
*講師の先生から,
● 使用教材:
*新興出版社 啓林館発行 高校教科書 「数学活用」(550円)
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/
第15回総会および特別講演会を開催いたします。
講演のタイトルが決まりましたので、合わせてお知らせいたします。
日時 : 平成28年5月22日(日)
理事会 午前11時30分 ~ 午後12時00分
総 会 午後12時00分 ~ 午後12時30分
特別講演会 午後 1時30分 ~ 午後 4時00分(予定)
※総会受付開始 午前11時15分~
会場 : 大東文化会館ホール (東京都板橋区徳丸2-4-21)
(東武東上線 「東武練馬」駅 下車)
議題 :
① 平成27年度事業活動報告(案)および同収支決算(案)について
② 平成28年度事業活動計画(案)および同収支予算(案)について
③ その他
総会終了後に講演会を開催いたします。講演のタイトル等は以下の通りになります。
《 特別講演について 》
(1) 『最近の暗号理論がめざしていること』
岡本 龍明氏(NTTセキュアプラットフォーム研究所室長)
(2) 『昔のガロア理論は何をめざしていたのか?』
加藤 文元氏(東京工業大学大学院理工学研究科教授)
是非ご参加いただき、今後の活発な活動にご協力をお願いいたします。
日本数学協会・国際教育学会共催 数学講座
「数学活用の教科書を読む<10回目>」
● 日時: 2016年3月26日(土) 15:00~17:00
● 会場: 正進社5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講師: 宮永 望,水谷 一,(上野健爾,有田八州穂)
● 講座内容:
*高校教科書「数学活用」の話題をもとに,その内容を講座形式で読み進めます。
*多方面に活用されている数学では,どのような理論が関係しているかを,楽しく
好奇心満載で学べます。
(例)数と計算の進化,新しい幾何学,優勝チームの決め方,無限とパラドックス,
音楽と数学,素数ゼミと暗号,世界のゲーム・パズル,どうやって議席が決まるかなど
*前回の講座に参加していなくても,新しくの参加は全く心配ありません。
*小・中・高校の先生には,単元導入時の話題提供や児童・生徒の興味関心のアッ
プにぴったりです。
● 講座詳細:
*毎回1/2~1単元ほど読み進めます。
*3月講座では,「美術館の順路を考える」から読み進めます。
*講師の先生から,その単元に関係する独自の資料が配付されます。
● 使用教材:
*新興出版社 啓林館発行 高校教科書 「数学活用」(550円)
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
「数学活用の教科書を読む<9回目>」
● 日時: 2016年2月27日(土) 15:00~17:00
● 会場: 正進社 5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講師: 宮永 望、水谷 一、(上野健爾、有田八州穂)
● 講座内容:
*高校教科書「数学活用」の話題をもとに、
*多方面に活用されている数学では、
心満載で学べます。
(例)数と計算の進化、新しい幾何学、優勝チームの決め方、
音楽と数学、素数ゼミと暗号、世界のゲーム・パズル、
*前回の講座に参加していなくても、
*小・中・高校の先生には、単元導入時の話題提供や児童・
● 講座詳細:
*毎回1/2~1単元ほど読み進めます。
*2月講座では、1月講座に引き続き、「新しい幾何学」
*講師の先生から、
● 使用教材:
*新興出版社 啓林館発行 高校教科書 「数学活用」(550円)
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/
数学講座
● 日時: 2016年1月30日(土) 15:00~17:00
● 会場: 正進社 5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール
(正進社HP http://www.seishinsha.co.jp)
● 講師: 宮永 望、水谷 一、(上野健爾、有田八州穂)
● 講座内容:
*高校教科書「数学活用」の話題をもとに、
*多方面に活用されている数学では、
(例)数と計算の進化、新しい幾何学、優勝チームの決め方、
*前回の講座に参加していなくても、
*小・中・高校の先生には、単元導入時の話題提供・
● 講座詳細:
*毎回1~2単元ほど読み進めます。
*2016年1月講座では、前回に引き続き、「新しい幾何学」
*講師の先生から、
● 使用教材:
*新興出版社 啓林館発行 高校教科書 「数学活用」(550円)
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/
数学講座
● 日時: 2016年1月30日(土) 15:00~17:00
● 会場: 正進社 5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール
(正進社HP http://www.seishinsha.co.jp)
● 講師: 宮永 望、水谷 一、(上野健爾、有田八州穂)
● 講座内容:
*高校教科書「数学活用」の話題をもとに、
*多方面に活用されている数学では、
(例)数と計算の進化、新しい幾何学、優勝チームの決め方、
*前回の講座に参加していなくても、
*小・中・高校の先生には、単元導入時の話題提供・
● 講座詳細:
*毎回1~2単元ほど読み進めます。
*2016年1月講座では、前回に引き続き、「新しい幾何学」
*講師の先生から、
● 使用教材:
*新興出版社 啓林館発行 高校教科書 「数学活用」(550円)
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/
日本数学協会、 東京大学素粒子物理国際研究センター、
四日市大学関孝和数学研究所の共催により新春特別講義
を下記のように開催しますのでご案内します。
今回はこれまでの新春特別講義と曜日、開始時間が異なりますのでご注意下さい。
日時 2016年1月10日(日) 〜11日(月)
場所 東京大学小柴ホール(本郷キャンパス理学部1号館)
(http://www.u-tokyo.ac.jp/campusmap/cam01_00_25_j.html)
プログラム
1月10日(日) 10:00〜11:30
講師:小林富雄(東京大学名誉教授)
「物理と数学と音楽 ― 分類と統合」
13:00〜14:30
講師:桂 利行(法政大学理工学部経営システム工学科)
「楕円関数が綾なす世界——— 算術・幾何・物理」
15:00〜16:30
講師:清水勇二(国際基督教大学教養学部)
「行列の標準形をめぐって」
1月11日(月) 10:00〜11:30
講師:上野健爾(四日市大学関孝和研究所)
「様々な幾何学」
受講料:学生(含む大学生)無料 社会人1000円
参加資格:どなたでも参加できます(部分参加も可)
募集人員:約150名(先着順)
応募方法:往復はがきに住所、氏名、学校名(学生の場合は学年も)または勤務先および電話番号明記の上、
返信はがきに自分のあて先を書いて下記までお送りください。12月25日までに必着のこと。(先着順受付)
〒160-0022
東京都新宿区新宿2-3-16
ライオンズマンション御苑前504号室
四日市大学関孝和数学研究所東京分室
新春特別講義係
問合わせ先:四日市大学関孝和数学研究所東京分室 TEL&Fax03-5925-8347
(宿泊の世話はできかねますのでご了承ください)
数学講座
「数学活用の教科書を読む<7回目>」
● 日時: 2015年12月5日(土) 15:00~17:00
● 会場: 正進社 5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講師: 宮永 望、水谷 一、(上野健爾、有田八州穂)
● 講座内容:
*高校教科書「数学活用」の話題をもとに、
*多方面に活用されている数学では、
(例)数と計算の進化、新しい幾何学、優勝チームの決め方、
*前回の講座に参加していなくても、
*小・中・高校の先生には、単元導入時の話題提供・
● 講座詳細:
*毎回1~2単元ほど読み進めます。
*12月講座は、今回は「新しい幾何学」を読みます。
11月講座に参加なさった方は、
(新参加者用の資料も準備します。)
*講師の先生から、
● 使用教材:
*新興出版社 啓林館発行 高校教科書 「数学活用」(550円)
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/
● 懇親会・忘年会
*12月講座の終了後、懇親会を兼ねた忘年会を行います。
数学講座
「数学活用の教科書を読む<6回目>」
● 日時: 2015年11月7日(土) 15:00~17:00
● 会場: 正進社 5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講師: 宮永 望、水谷 一、(上野健爾、有田八州穂)
● 講座内容:
*高校教科書「数学活用」の話題をもとに、
*多方面に活用されている数学では、
(例)数と計算の進化、新しい幾何学、優勝チームの決め方、
音楽と数学、素数ゼミと暗号、
*前回の講座に参加していなくても、
● 11月講座のご案内:
*11月講座は、教科書の「パソコンで学ぶ幾何学」
*講師の先生から、
● 使用教材:
*新興出版社 啓林館発行 高校教科書 「数学活用」(550円)
● 会場地図: 下記の正進社ホームページにてご確認下さい。
● 講座へ参加される方は、伊藤までご連絡願います。
日本数学協会・国際教育学会共催
数学講座
「数学活用の教科書を読む<5回目>」
● 日時: 2015年10月3日(土) 15:00~17:00
● 会場: 正進社 5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講師: 宮永 望、水谷 一、(上野健爾、有田八州穂)
● 講座内容:
*高校教科書「数学活用」の話題をもとに、
*多方面に活用されている数学では、
(例)数と計算の進化、新しい幾何学、優勝チームの決め方、
世界のゲーム・パズル、どうやって議席が決まるか など
*前回の講座に参加していなくても、
*小・中・高校の先生には、単元導入時の話題提供・
● 講座詳細:
*毎回1~2単元ほど読み進めます。
*10月講座は、「もっと自由に考える(2)」
*講師の先生から、
(10月は、8月の資料を使います。8月に参加された方は、
● 使用教材:
*新興出版社 啓林館発行 高校教科書 「数学活用」(550円)
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/
● 参加希望者は、正進社伊藤まで、メール等でご連絡願います。
『国際教育学会第10回大会』及び公開シンポジウムにつきまして、下記の要領での開催が決まりましたので、御案内申し上げます。
ご多忙のところ誠に恐縮でございますが、ご出席頂きますようお願い申し上げますとともに、
下記の参加お申込書書式にご記入のうえ、7月末日までにご返信・ご返送いただきますよう、心よりお願い申し上げます。
・問い合わせ先: 国際教育学会事務局(担当:井上)
・TEL: 075-753-7184 E-mail: ise@sfi-npo.net
・ホームページ: http://sfi-npo.net/ise/
詳細につきましては、下記添付資料をご参照ください。
国際教育学会(大会プログラム・申し込み).pdf
公開シンポジウム詳細.pdf
第13回年次大会を下記の通り開催いたします。例年より早い開催となります。
日時: 8月22日(土)午前10:30~
場所: 東京大学数理科学研究科棟(駒場) (京王井の頭線「駒場東大前」)
<午前の部>
*** 特別記念講演 ***
10:30~11:30 「算額を世界文化遺産に」 (仮題)
小林 龍彦氏 (四日市大学関孝和数学研究所)
<昼休み>ポスターセッション
<午後の部>
*** ワークショップ ***
① 13:15~14:15 「帰除法について」 太田 敏幸氏(珠算史研究学会会長)
② 14:30~16:30 「展開図変身マジック」 宮永 望氏(数学教師・日本数学協会幹事)
※当日は、はさみとセロハンテープをご持参ください。ワークショップで使用いたします。
≪ポスターセッション≫
l 鈴木啓一氏 『マイナス微分の定義⇒ローラン展開の主要部を実数で定義』
l 本荘光史氏 『リーマン予想、未知の登頂ルート』
(私の仮説、素粒子脈動原理による証明)
l 貴田研司氏 『ある情報系学科の大学新入生を対象とした定理・公式の適用能力調査』
l 室井正史氏 『シュワルツシルトの計量によるエネルギーの式の検証』
l 深山順夫氏 『「これって解なのね」
ブラジルナッツ効果(粒度偏析)における幾何学的な意味(実演あり)』
なお、参加料は、会員が1,000円、非会員が2,000円になります。
(但し、大学生、高校生および引率者の教師、父母も無料になっています)。
準備の都合上、ご参加ご希望の方は、メールまたはファックス、郵送にて事前に事務局宛にご連絡をお願い申し上げます。
≪お詫びと訂正≫
会員の皆様に送付いたしました、『第13回年次大会の開催のご案内』におきまして、事務局宛のファックス番号に誤りがございました。申し訳ございませんでした。
FAX:03-5269-8182 が正しい番号になります。宜しくお願いいたします。
【本件担当】 日本数学協会 事務局
〒160-0011 東京都新宿区若葉1-10
℡: 03-6821-3313 FAX: 03-5269-8182
E-Mail: sugakubunka@gmail.com
第14回総会が東京大学数理科学研究科棟にて、平成27年6月7日に行われました。
平成26年度事業活動報告、同収支決算、同じく平成27年度事業活動計画、および同収支予算について慎重にご審議頂き、
無事原案通り、全て承認されましたのでご報告いたします。
総会議事録.pdf
今年も数学月間(7/22~8/22)が近づきました.
この時期に,
今年の懇話会のご案内です.ご参加をお待ちしております.
------記----
数学月間懇話会(第11回)
主催●日本数学協会,数学月間の会(SGK)
日時●7月22日,13:50-17:20
----
1.十年目の「数学月間」
片瀬豊,高窪正明(SGK)
2.「サッカーボールの対称性を解くTopological Symmetry」
細矢治夫(お茶の水女子大名誉教授)
3.繰り返し模様の観賞法
谷克彦(SGK)
4.テーラー展開の話
鈴木啓一(SGK)
ーーーー
会場●東京大学(駒場)数理科学研究科棟002号室
最寄り駅●京王井の頭線「駒場東大前」
参加費●無料
問合せ先●数学月間の会(SGK)
sgktani@gmail.com,谷克彦(SGK世話人)
直接会場においでください(開場13:30)
17:30より構内で各自払いの懇親会も予定しています.
詳細は http://sgk2005.sakura.ne.jp をご覧ください.
無料メルマガ(まぐまぐ!)「数学月間SGK通信」
$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$
ICUオープンキャンパスでのモデル授業
題目:シンメトリー - 現代数学への扉
講師:清水勇二
日時:8月8日(土) 12:05~12:50 および 15:05~15:50
(同じ講義を2回します。)
場所:国際基督教大学 本館3F 316 教室
(東京都三鷹市大沢 3-10-2)
数学講座
「数学活用の教科書を読む<4回目>」
● 日時: 2015年8月8日(土) 15:00~17:00
● 会場: 正進社 5階会議室
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講師: 宮永 望、水谷 一、(上野健爾、有田八州穂)
● 講座内容:
*高校教科書「数学活用」の話題をもとに、
*多方面に活用されている数学では、
(例)数と計算の進化、新しい幾何学、優勝チームの決め方、
世界のゲーム・パズル、どうやって議席が決まるか など
*前回の講座に参加していなくても、
*小・中・高校の先生には、単元導入時の話題提供・
● 講座詳細:
*毎回1~2単元ほど読み進めます。
*8月は、「もっと自由に考える(1)」
*講師の先生から、
● 使用教材:
*新興出版社 啓林館発行 高校教科書 「数学活用」(550円)
● 会場地図: 下記の正進社ホームページにてご確認下さい。
● 参加希望者は、正進社伊藤まで、メール等でご連絡願います。
◆数学文化講演会のご案内
---- 東北支援 第4回数学文化講演会 in 山形 ----
本年度日本数学協会強化事業の一環として下記講座を開講致します。
奮ってお出かけください。
v 日時 平成27年7月12日(日)(10:00 開場) 10:30開演
v 場所 山形大学小白川キャンパス理学部先端科学実験棟401教室
v 入場 無料(高校生向けですが一般の方も受け付けます。途中どこからも参加可)
v 主催 日本数学協会
v 共催 四日市大学関孝和数学研究所
v 後援 山形大学理学部 山形県教育委員会
v プログラム
10:30 ~12:00 森田康夫氏 「入試問題と数学の勉強法」
(昼食休憩)
13:30 ~15:00 桂 利行氏 「相加平均と相乗平均を使いこなす」
15:15 ~16:45 上野健爾氏 「複素数の世界」
数学講座
「数学活用の教科書を読む<3回目>」
● 日時: 2015年6月27日(土) 15:00~17:00
● 会場: 正進社 5階会議室
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講師: 宮永 望、水谷 一、(上野健爾、有田八州穂)
● 講座内容:
*高校教科書「数学活用」の話題をもとに、
*多方面に活用されている数学では、
(例)数と計算の進化、新しい幾何学、優勝チームの決め方、
世界のゲーム・パズル、どうやって議席が決まるか など
*前回の講座に参加していなくても、
*小・中・高校の先生には、単元導入時の話題提供・
● 講座詳細:
*毎回1・2単元ほど読み進めます。
*6月は、「2進法のしくみ」の単元から読み進めます。
*講師の先生から、
● 使用教材:
*新興出版社 啓林館発行 高校教科書 「数学活用」(550円)
● 会場地図: 下記の正進社ホームページにてご確認下さい。
● 参加希望者は、正進社伊藤まで、メール等でご連絡願います。
第14回総会および講演会を開催いたします
日時:平成27年6月7日(日)
総 会 :午前11時30分 ~ 午後12時30分
講演会 : 午後 1時30分 ~ 午後 3時40分(予定)
※総会受付開始 午前11時15分~
会場:東京大学数理化学研究科棟 (東京都目黒区駒場3-8-1)
(京王井の頭線 「駒場東大前」 下車)
議題:
① 表彰状贈呈
② 幹事会からの報告
③ 平成26年度事業活動報告(案)および同収支決算(案)について
④ 平成27年度事業活動計画(案)および同収支予算(案)について
⑤ その他
なお、やむを得ずご欠席なさる方は、必ず5月29日(金)までに委任状を
FAX,E-mail、郵送等で事務局までお送りくださいますようお願いいたします。
また、総会終了後に講演会を開催いたします。詳細は下記の通りです。
《 講演会について 》
(1) 『10年目の数学月間、これまでとこれから』 午後1時30分~午後2時30分
片瀬 豊氏(数学月間の会)
谷 克彦氏(数学月間の会)
-----10分休憩-----
(2) 『視覚と錯視の数学からアート、そして画像処理』 午後2時40分~午後3時40分
新井 仁之氏(東京大学大学院数理科学研究科)
是非ご参加いただき、今後の活発な活動にご協力をお願いいたします。
数学講座
「数学活用の教科書を読む<2回目>」
● 日時: 2015年5月30日(土) 15:00~17:00
● 会場: 正進社 5階会議室
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講師: 宮永 望、水谷 一、(上野健爾、有田八州穂)
● 講座内容:
*高校教科書「数学活用」の話題をもとに、
*多方面に活用されている数学では、
(例)数と計算の進化、新しい幾何学、優勝チームの決め方、
世界のゲーム・パズル、どうやって議席が決まるか など
*4月の講座に参加していなくても、
*小・中・高校の先生には、単元導入時の話題提供・
● 講座詳細:
*毎回2単元ほど読み進めます。
*5月は、「地球を測る[1]」の単元から読み進めます。
*講師の先生から、
● 使用教材:
*新興出版社 啓林館発行 高校教科書 「数学活用」(550円)
● 会場地図: 下記の正進社ホームページにてご確認下さい。
● 参加希望者は、正進社伊藤まで、メール等でご連絡願います。
「数学活用の教科書を読む<1回目>」
● 日時: 2015年4月25日(土) 15:00~17:00
● 会場: 正進社 5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
*高校教科書「数学活用」の話題をもとに、その数学の内容を講座
講座では、聴講者は,自由に質問や感想を発言できます。
*4月は、新たな講座開始です。初めからの学習が可能です。
■数学入門講座■
「遠山啓の数学入門を読む<第24回(総集編)>」
● 日時: 2015年3月14日(土) 15:00~17:00
● 会場: 正進社 5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、
聴講者は,自由に質問や感想を発言できます。
初めての方でも,途中からの参加の方でも、
● 3月第24回の講座は、総集編です。上・
具体的には,
・第9章:交わりと結び、ベズーの定理
・第10章:数学的帰納法、階差 などです。
過去の資料をお持ちの方は、持参願います。
時間がとれれば、上・下巻の全体についての質問も受けます。
● 講師: 宮永 望、水谷 一、(上野健爾、新井 紀子、有田八州穂)
● 準備するもの: 遠山啓著「数学入門(上・下巻)」岩波新書
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/
● 申し込み方法:
参加申し込みメールを、正進社伊藤まで(t-ito@
● 今後の予定:
4月以降の講座内容と講座日程は未定です。
決まりましたら,後日ご連絡いたします。
**************************************
平成26年度 観光政策Informix のお知らせ
毎年恒例の観光政策学科のイベントも7回目を迎えます。
今回は学生の発表に加え、長年山口大学でご活躍された宮崎先生の最終講義とシューマン先生の特別講義を開催します。
入場無料ですので、どなたでもご自由にご参加ください。
日時:平成27年1月14日
会場:山口大学経済学部C201教室
http://www.yamaguchi-u.ac.jp/info/13/68.html
プログラム:
第一部 宮崎充保 教授 最終講義
演題「コミュニケーションとしての翻訳」
14:30-15:30(予定)
第二部 フレッド・シューマン先生(グアム大学) 特別講義
演題「グアムの観光と教育」
15:30-16:30(予定)
第三部 観光政策学科の学生によるプレゼン
プロジェクト演習1(国内研修)の優秀プレゼン
プロジェクト演習2(海外研修)の優秀プレゼン
16:30-17:30(予定)
問い合わせ先:
朝水(masamizu@yamaguchi-u.ac.jp)
****************************************************
国際教育学会(ISE) 事務局
〒606-8501
京都市左京区吉田本町 京都大学経済研究所内
Tel: 075-753-7184
E-mail: ise@sfi-npo.net
Homepage: http://sfi-npo.net/ise/
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む<23回目>」
● 日時: 2015年1月31日(土) 15:00~17:00
● 会場: 正進社 5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、
せ講座形式で行い,数学に対する理解を深めます。
聴講者は,自由に質問や感想を発言できます。
初めての方でも,途中からの参加の方でも、
● 新年1月講座では、下巻の最終章「微視の世界--微分方程式」
読 み進めます。
● 講師: 宮永 望、水谷 一、(上野健爾、新井 紀子、有田八州穂)
● 準備するもの: 遠山啓著「数学入門(下)」岩波新書
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/
● 申し込み方法:
参加申し込みメールを、正進社伊藤まで(t-ito@
● 今後の予定:
第24回予定:2015年3月の土曜日を予定しております。
講座のくわしい内容・日程は,後日ご連絡いたします。
お問い合わせに関しては、国際教育学会(ISE)事務局様までお願いいたします。
***************************************
「2015年度 国際教育学会(ISE)第10回年次大会」研究発表募集のご案内
新年明けましておめでとうございます。
会員並びに関係者の皆様におかれましては、日々益々ご清祥のこととお慶び申し上げます。
国際教育学会(ISE) 第10回年次大会の研究発表の募集につきまして、お知らせ致します。
今年度の国際教育学会第10回大会は、2015年8月8日(土)に、
同志社大学(京都市左京区)にて「学びを科学する」という題名で開催する予定で準備を進めております(詳細はまた別途ご案内をさせていただきます)。
また同日には、京都大学経済研究所等との共催の公開シンポジウムを開催致します。
本大会におきまして、皆様が日ごろ、教育に関する研究、実践、お考えになられていることなどをご発表いただき、学び合う場をつくりたいと思います。
第10回大会での研究発表を希望される方は、下記の「発表会申込方法」をご覧いただき、ご応募下さい。
また国際教育学会は優れた実践を応援いたします。皆様のお知り合いで優れた実践者がいらっしゃいましたら、是非お知らせください。
締め切りは、2015年2月15日必着です。
ise@sfi-npo.net 宛てにメール添付書類にてお送りください。
皆さまのご応募・ご参加を心よりお待ち申し上げます。
☆☆☆☆☆☆ 記 ☆☆☆☆☆☆
「第10回国際教育学会(ISE)年次大会 研究発表会の申込方法につきまして」
○日時 2015年8月8日(土) 午後1時30~13時00分(予定)
○会場 同志社大学 寒梅館
(詳細は別途ご連絡いたします)
○発表時間
持ち時間は 15分~20分程度(質疑応答含む)を予定しております。
○発表申込方法
2015年2月15日(木) までに、下記内容をE-mail (ise@sfi-npo.net)にてご送付下さい。
※E-mail送信が不可の場合はFAX送信(075-753-7157)してください。
1 )発表者の氏名、所属
※発表者が複数の場合、すべての方の氏名・所属機関をお書きください。
2 )発表者(代表者)の連絡先
氏名
住所:〒
TEL:
FAX:
E-mail:
※発表者が複数の場合、代表者の方のみの連絡先をお書きください。
3 )発表タイトル(発表の区分)
※発表の区分は、1. 研究発表、2. 実践報告、3. 問題提起 のいずれかをお選び下さい。
4 )発表要旨:(200字程度)
○申込締切
2015年2月15日必着
○申し込まれた発表タイトルと要旨の査読とその結果の通知について
発表申し込み多数の場合は、発表タイトル、および要旨にもとづいて査読を行い、2月20日までに結果をご通知いたします。
なお、ご発表頂く方には、7月15日までに論文のPDFファイルを、
7月31日までにプレゼンテーション用のファイル(パワーポイントなど)をE-mailにて送付頂きますようお願い致します。
○申込先
E-mail送信: ise@sfi-npo.net
FAX送信: 075-753-7157
○問合せ先
国際教育学会(ISE)事務局
〒606-8501 京都市左京区吉田本町
京都大学経済研究所内(担当:青木)
TEL: 075-753-7184
≪ 高校生と社会人のための現代数学・物理学入門講座 ≫
日本数学協会、四日市大学関孝和数学研究所、 東京大学素粒子物理国際研究センターの共催により
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む<22回目>」
● 日時: 2014年12月27日(土) 15:00~17:00
● 会場: 正進社 5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わ
せ講座形式で行い,数学に対する理解を深めます。
聴講者は,自由に質問や感想を発言できます。
初めての方でも,途中からの参加の方でも、聴講は心配ありません。
● 12月講座では、下巻の最終章「微視の世界--微分方程式」の続き(2回目)を読み進めます。
● 講師: 宮永 望、水谷 一、(上野健爾、新井 紀子、有田八州穂)
● 準備するもの: 遠山啓著「数学入門(下)」岩波新書
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にてお
知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生
の方、企業等の方)
● 今後の予定:
第23回予定:2015年1月または2月
講座のくわしい内容・日程は,後日ご連絡いたします。
【忘年会のお知らせ】
12月講座修了後、数学講座参加者の懇親会・忘年会を開きます。
日頃聞けなかったこと、相談したかったことなど、お酒を飲みながら、楽しく語り合いましょう。
(会費4000円程度、申し込みの方は伊藤まで早めの連絡をお願いします。)
2015年8月8日(土曜日)同志社大学今出川キャンパスにて開催されることになりましたので、
ここに謹んでお知らせ申し上げます。
学び合う場として、研究発表会をおこないたいと存じます。
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む<21回目>」
● 日時: 2014年11月29日(土) 15:00~17:00
● 会場: 正進社 5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い,数学に対する理解を深めます。
聴講者は,自由に質問や感想を発言できます。
初めての方でも,途中からの参加の方でも、聴講は心配ありません。
● 11月講座では、下巻の最終章「微視の世界--微分方程式」に入り、読み進めます。
● 講師: 上野健爾、宮永 望、水谷 一、有田八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(下)」岩波新書
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にてお知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第22回予定:2014年12月中
講座のくわしい内容・日程は,後日ご連絡いたします。
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む<20回目>」
● 日時: 2014年10月25日(土) 15:00~17:00
● 会場: 正進社 5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い,数学に対する理解を深めます。
聴講者は,自由に質問や感想を発言できます。
初めての方でも,参加・聴講は心配ありません。
10月の講座では、前回の9月講座に引き続き、第13章「総合の方法――積分」の続きを読み進める予定です。
● 講師: 上野健爾、宮永 望、水谷 一、有田八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(下)」岩波新書
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にてお知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第21回予定:2014年11月中
講座のくわしい内容・日程は,後日ご連絡いたします。
第13回総会が大東文化会館ホールにて、平成26年6月1日に行われました。
平成25年度事業活動報告、同収支決算、同じく平成26年度事業活動計画、および同収支予算について慎重にご審議頂き、
無事原案通り、全て承認されました。
第12回年次大会が東京大学数理科学研究科棟講義室にて、平成26年9月14日におこなわれました。
特別記念講演の終了後に、臨時総会が開催され、平成27年度以降の新役員の選出について審議をおこない、無事原案通り承認されました。
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む<19回目>」
● 日時: 2014年9月27日(土) 15:00~17:00
● 会場: 正進社 5階 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い,数学に対する理解を深めます。
聴講者は,自由に質問や感想を発言できます。
初めての方でも,参加・聴講は心配ありません。
○9月の講座では、前回の8月講座に引き続き、第13章「総合の方法――積分」(基本定理以降)を読み進める予定です。
● 講師: 上野健爾、宮永 望、水谷 一、有田八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(下)」岩波新書
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にてお知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第20回予定:2014年10月中
講座のくわしい内容・日程は,後日ご連絡いたします。
第12回年次大会を開催のお知らせ
開催日時:平成26年9月14日(日)
会場:東京大学駒場キャンパス 数理科学研究科
10:00 開会挨拶
10:05 特別記念講演
「『大成算経』に蒐集された珠算法 」 小川 束氏 (四日市大学)
(質疑応答を含む)
11:30 臨時総会
議題 平成27年度以降の新役員の選出について
12:00 お昼休憩
《ポスターセッション》
l 鈴木啓一氏 『無限大での微分の意味は?』
l 松田康雄氏 『円と2次曲線と(続)』
l 野上 勉氏 『魔方陣に秘められていた力学特性』
l 武 純也氏 『続 紙鎖立方体』
l 深山順夫氏 『似て非なる2ωと2ω数直線上の位置を
2進表示することの意味』
l 藤森弘章氏 『平面の対称性とユークリッド幾何学の拡張』
l 貴田研司氏 『ある情報系学科1学年前期終了時における
数学学力と入試方式』
l 山本文隆氏 『フェルマーの最終定理の簡易証明』
l 室井正史氏 『エネルギーの式』
l 寺尾 敦氏 『ランダムウォークの性質についての大学生の直感的理解』
太田梨沙子氏(学生)
本仲ひより氏(学生)
13:00 ワークショップ
① 「どのように使ったの “五珠2つそろばん”」
太田 敏幸氏 (珠算史研究学会 会長)
② 「算木を使って2次方程式を解いてみよう」
上野 健爾氏 (関孝和数学研究所長)
15:00 閉会挨拶
なお、参加費は会員1,000円、会員外2,000円となります。
(但し、大学生、高校生および引率者の教師、父母も無料になっています。)
奮ってご参加下さい。
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む<19回目>」
● 日時: 2014年8月23日(土) 15:00~17:00
● 会場: 正進社 5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い,
数学に対する理解を深めます。
聴講者は,自由に質問や感想を発言できます。初めての方でも,参加・聴講は心配ありません。
○8月講座は,いよいよ下巻の第13章(総合の方法-積分)に入ります。
● 講師: 上野 健爾、宮永 望、水谷 一、有田八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(下)」岩波新書
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にてお知らせくださいます
ようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第20回予定:2014年9月中 講座のくわしい内容・日程は,後日ご連絡いたします。
日本数学協会・国際教育学会共催
■数学入門講座■
【特別講義】考える楽しみ
「数学問題を楽しく解き合いましょう」
● 日時: 2014年7月19日(土) 15:00~17:00
● 会場: 正進社 5階 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 特別講義で解きあう問題
水谷 一先生出題
2013 年数学月間懇話会の講演(http://www.sugaku-bunka.org/jojcoqr1e-453/#_453) で扱った問題を、参加の方々に考えていただき,講師が解説します.
数学入門講座 特別講義(2014/07/19).doc
聴講者は,自由に質問や感想を発言できます。初めての方でも,参加・聴講は心配ありません。
○ なお,8月の講座は,下巻の第13章(総合の方法-積分)に入ります。
● 講師: 上野 健爾、宮永 望、水谷 一、有田 八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(下)」岩波新書
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にてお知らせくださいます
ようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第19回予定:2014年8月23日(土)予定 下巻第13章(総合の方法-積分)
日本数学協会会員の皆様へ
今年も数学月間(7/22~8/22)が近づきました.
この時期に,色々な数学イベントが各地で隆盛になることを願っています.
さて、今年の懇話会は以下のように進めています.ぜひご参加ください.
数学月間懇話会(第10回)
日時 7月22日(火) 14:00-17:10
1. 人口の集合関数としての「民力指数」
松原望(東京大学名誉教授,聖学院大学)
2. スパゲッテイを巡る旅,
中西達夫(株・モーション)
3. 数学月間の狙と効用,今年の米国MAM
片瀬豊,谷克彦(日本数学協会)
会場 東京大学(駒場)数理科学研究科棟,002号室
最寄り駅 京王井の頭線「駒場東大前」
参加費 無料
問合せ先 日本数学協会,数学月間の会(SGK)
sgktani@gmail.com,谷克彦(SGK世話人)
詳細は http://sgk2005.sakura.ne.jp をご覧ください.
無料メルマガ(まぐまぐ!)「数学月間SGK通信」も発行しています.
直接会場においでください(開場13:30).ご参加お待ちしています.
17:30より構内で各自払いの懇親会も予定しています.
◆数学文化講演会のご案内
本年度日本数学協会強化事業の一環として下記講座を開講致します。
奮ってお出かけください。
○日時 平成26年6月28日(土)
○場所 山形大学理学部 山形県山形市小白川町1丁目4-12
※事前登録は必要ありませんので、出席希望の方は当日会場までおいでください。
参加費は無料です。
○プログラム
10:00 ~11:30 森田康夫氏 「素因数分解の一意性とその応用」
12:30 ~14:00 清水勇二氏 「多項式をめぐるはなし三話」
14:15 ~15:30 上野健爾氏 「合同式に親しもう ― 継子立てと合同式― 」
15:45 ~17:15 桂 利行氏 「大きな素数の応用― RSA暗号」
また、総会終了後に講演会を予定しております。
《講演会について》
*13:45~14:35 「建部賢弘生誕350周年を記念して(仮)」
講演者 森本 光生氏(四日市大学関孝和数学研究所)
*14:45~15:35 「建部賢弘をめぐって」
講演者 鳴海 風氏(作家)
*15:45~16:35 「建部賢弘とそろばん」
講演者 小川 束氏(四日市大学)
是非、ご参加ください。
〒160−0011
東京都新宿区若葉1-10
TEL:03−6821−3313
FAX:03−5269−8182
E-Mail:sugakubunak@gmail.com
《訂正とお詫び》
先日送付いたしました会報(第45号)におきまして、誤記がございました。
誠に申し訳ございませんが、訂正をお願い申し上げます。
『事務局からのお願い』に記載しております口座番号の記載が間違っておりました。
正しくは、
口座番号 00100-3-574354
になります。 訂正し、お詫び申し上げます。
5月25日(日)午後2時より、同志社大学創造経済研究センター主催(共催:国際教育学会(ISE)他)により、
同志社大学室町キャンパス寒梅館ハーディーホールにおきまして、
公開シンポジウム「目指すべき未来社会と望ましい人材育成政策~スポーツとアートの可能性~」を開催致しますのでご案内申し上げます。
詳細は添付のチラシをご覧ください。5月25日 公開シンポジウムチラシ.pdf
国際教育学会(ISE)からも、西村和雄会長、八木匡副会長が出席されます。
皆様奮ってご参加くださいますよう、心よりお願い申し上げます。
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む<16回目>」
● 日時: 2014年5月24日(土) 15:00~17:00
● 会場: 正進社 5階 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い,
数学に対する理解を深めます。
聴講者は,自由に質問や感想を発言できます。初めての方でも,参加・聴講は心配ありません。
○5月講座は,下巻の第12章(分析の方法-微分)を学ぶ2回目の講座です。
第12章の中・後半の内容を読み進める予定です。
● 講師: 上野 健爾、宮永 望、水谷 一、有田 八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(下)」岩波新書
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にてお知らせくださいます
ようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第17回予定:2014年6月中 講座のくわしい内容・日程は,後日ご連絡いたします。
是非ご参加をご検討ください。
参加費はすべて無料です.詳細はSGK通信(2014-06)をご覧下さい.
◆情報環境と人
~「突き抜ける」さきがけ研究の成果から ~
日時:3月1日(土)14:00~17:15
◆数学連携ワークショップ
---生命科学、材料科学における数理---
日時3月16日(日)9:30-12:00
◆日本学術会議公開シンポジウム
「数理モデリング(数学と諸科学・産業との連携の観点から)」
日時:2014年3月26日(水)13:00-17:30
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む<15回目>」
● 日時: 2014年3月8日(土) 15:00~17:00
● 会場: 正進社 5階 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い,
数学に対する理解を深めます。
聴講者は,自由に質問や感想を発言できます。初めての方でも,参加・聴講は心配ありません。
○3月講座は第15回目になります。15回目からの2~3回で,下巻の第12章(分析の方法-微分)の
内容のすべてを読む予定です。
● 講師: 上野 健爾、宮永 望、水谷 一、有田 八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(下)」岩波新書
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にてお知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第16回予定:2014年5月中 講座のくわしい内容・日程は,後日ご連絡いたします。
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む<14回目>」
● 日時: 2014年1月25日(土) 15:00~17:00
● 会場: 正進社 5階 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い,
数学に対する理解を深めます。
聴講者は,自由に質問や感想を発言できます。初めての方でも,参加・聴講は心配ありません。
○第14回目は,13回目の内容の続きで,下巻第11章(主に「分数の指数」「指数関数」
「対数」「連続複利法」「オイレルの公式」)を読みます。
● 講師: 上野 健爾、宮永 望、水谷 一、有田 八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(下)」岩波新書
※通常の1回の講座では,1/2章~1章ほどを読み進めています。
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にて
お知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第15回予定:2014年2月中 講座のくわしい内容・日程は,後日ご連絡いたします。
四日市大学関孝和数学研究所、東京大学素粒子物理国際研究センターと日本数学協会の共催により
新春特別講義「幾何の世界」を以下の要領で開催しますのでご案内します。
タイトルは仮のもので変更されることがあります。
1月11日(土) 13:30~15:00
講師:上野健爾(四日市大学関孝和研究所)
「三平方の定理から超弦理論へ」
15:15~16:45
講師:桂 利行(法政大学理工学部経営システム工学科)
「素粒子は代数幾何の世界を飛ぶか」
1月12日(日) 10:00~11:30
講師:徳永浩雄(首都大学東京 大学院理工学研究科)
「曲がった空間とやわらかい幾何」
13:00~14:30
講師:清水勇二(国際基督教大学教養学部)
「リーマン幾何学:テンソルと接続をめぐって」
14:45~16:15
講師:小林富雄(東京大学素粒子物理国際研究センター)
「素粒子と幾何学」
会場
東京大学小柴ホール(本郷キャンパス理学部1号館)
受講料 学生(含大学生)無料、 社会人1000円
参加資格 どなたでも参加できます。部分参加も可。 (宿泊の世話は出来かねますのでご了承下さい。)
募集人員 約150名
応募方法 往復はがきに住所、 氏名、 学校名 (学生の場合は学年も記してく ださい) または勤務先、
および電話番号を明記の上、 返信用はがきに応募者の 宛先を書いて
〒160-0022 東京都新宿区新宿 2-3-16 ライオンズマンション504
関孝和数学研究所東京分室 新春特別講義係
Fax 03-5925-8347
に 12 月 20 日までに必着のこと。 受講者は原則として先着順に受け付けます。
返信用はがきは受講票になります。
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む<13回目>」
● 日時: 2013年12月21日(土) 15:00~17:00
● 会場: 正進社 5階 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い,
数学に対する理解を深めます。
聴講者は,自由に質問や感想を発言できます。初めての方でも,参加・聴講は心配ありません。
○第13回目は,下巻第11章(主に「分数の指数」「指数関数」「対数」「連続複利法」
「オイレルの公式」)を読みます。
● 講師: 上野 健爾、宮永 望、水谷 一、有田 八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(下)」岩波新書
※通常の1回の講座では,1/2章~1章ほどを読み進めています。
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にて
お知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第14回予定:2014年1月中 講座のくわしい内容・日程は,後日ご連絡いたします。
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む<12回目>」
● 日時: 2013年11月30日(土) 15:00~17:00
● 会場: 正進社 5階 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い,
数学に対する理解を深めます。
聴講者は,自由に質問や感想を発言できます。初めての方でも,参加・聴講は心配ありません。
○第12回目は,下巻第10章(主に「ある空想的なゲーム」「コーシーの収束条件」「収束と加減乗除」)
を読みます。(10月の講座予定と同じ内容です。)
● 講師: 上野 健爾、宮永 望、水谷 一、有田 八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(下)」岩波新書
※通常の1回の講座では,1/2章~1章ほどを読み進めています。
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にて
お知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第13回予定:12月21日(土)予定 講座のくわしい内容は,後日ご連絡いたします。
10月26日(土)に開催予定の数学講座ですが,台風の影響を考慮し,【中止】とさせていただきます。
今回の内容につきましては,予定しております,11月30日(土)に繰り越しとさせていただきます。
10月にご参加予定の方々には大変ご迷惑をおかけいたしますが,どうぞよろしくお願いいたします。
複雑系の研究で有名なサンタフェ研究所の創立者の1人で、後に、ネットワーク型複雑系研究所ICAMを創立者した
物理学者 David Pines サンタフェ研究所教授が科学教育の国際会議に出席のため、10月20日から京都を訪問されています。
10月20日には1時から京都大学時計台ホールで公開講座「科学を楽しもう」
http://sfi-npo.net/ise/information_html/2013_10_20_lecture.html
を、6時15分からウエスティン都ホテルで、GSEE/Kyoto Summit "Initiative That Can Change Science Education"、
http://sfi-npo.net/ise/information_html/2013_10_20_dailogue.html
を開きます。
公開講座出席、国際会議GSEE/Kyoto傍聴ご希望の方は、
公開講座「科学を楽しもう」へのご出席・国際会議GSEE/Kyoto傍聴のうちどちらをご希望か(両方ご出席も可能です)を明示のうえ、国際教育学会事務局
ise@sfi-npo.net
までメールにてご連絡ください。
なお、10月24日の4時から、Pines教授を囲んで学際的研究者が集まり、談話会を開催します。
そのあと、6時からPines教授と奥様を囲んで懇親会を開催します。
ちなみに、奥様は心理カウンセラーです。談話会(英語)、懇親会(6000円)ともに、フレンドリーな会にしたいと思いますので、
国際教育学会の会員の皆様で関心のある方は、是非ふるってご参加ください。
懇親会はラトゥールで予定していますが、参加者が増える場合には時計台2階会議室へ場所を変更する予定です。
参加ご希望の方は、24日の談話会・懇親会のうちどちらをご希望か(両方ご出席も可能です)を明示のうえ、国際教育学会事務局
ise@sfi-npo.net
までメールにてご連絡ください。
プログラム:
10月24日 GSEE, ICAM/Kyoto, ISE, 複雑系ユニット会合同談話会
場所:京都大学総合博物館本館3階 講演室
16:00- 16:40「思考の抑制にともなう大脳皮質ネットワークの挙動」
(イントロダクション:稲川三千代 京都大学大学院教育学研究科)
麻生俊彦 京都大学大学院医学研究科附属脳機能総合研究センター
16:50-17:30 「太陽でスーパーフレアは起きるのか?」
柴田 一成 京都大学大学院理学研究科附属天文台
18:00- 20:00懇親会
場所:ラトゥール(京都大学時計台記念館内1F)
会費:6000円
よろしくお願い申し上げます。
国際教育学会会長
西村和雄
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む<12回目>」
● 日時: 2013年10月26日(土) 15:00~17:00
● 会場: 正進社 5階 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い,
数学に対する理解を深めます。
聴講者は,自由に質問や感想を発言できます。初めての方でも,参加・聴講は心配ありません。
○第12回目は,下巻第10章(主に「ある空想的なゲーム」「コーシーの収束条件」「収束と加減乗除」)
を読みます。
● 講師: 上野 健爾、宮永 望、水谷 一、有田 八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(下)」岩波新書
※通常の1回の講座では,1/2章~1章ほどを読み進めています。
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にて
お知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第13回予定:11月30日(土)予定 講座のくわしい内容は,まだ決まっておりません。
第11回年次大会開催のおしらせ
日時:9月15日(日) 午前10時より
場所:東京大学数理科学研究科棟(駒場)
【プログラム】
《午前の部》
10:00 開会挨拶
10:05 ~特別講演~
「非常に小さい距離と非常に大きな距離でのみ世界は単純である」(同時通訳つき)
“The world is simple only at very small space-time distances”
ベルリンのフンボルト大学 J. ブリューニング教授による講演
(質疑応答含む)
12:00 お昼休憩
《午後のワークショップ》
13:00 A 世界に広がるそろばん 藤井將男先生
B 遠山啓の数学入門を読む (上巻部分の総集編) 宮永望先生
15:00 閉会挨拶
《ポスターセッション》につきましては、こちらをご覧ください。
ポスターセッション.pdf
なお、参加費は会員1,000円、会員外2,000円となります。
(但し、大学生、高校生および引率者の教師、父母も無料)になっています。奮ってご参加下さい。
『国際教育学会(ISE) 第8回大会』及び公開シンポジウムにつきまして、お知らせ致します。
■1.国際教育学会(ISE)第8回年次大会プログラム(予定)
☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆
【総会】
日 時: 2013年9月14日 (土) 13:00 ~13:20
会 場: 京都大学基礎物理学研究所 湯川記念館パナソニック国際交流ホール
主 催: 国際教育学会(ISE)
会長挨拶 (13:00 ~13:05)
総 会 (13:05 ~13:20)
☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆
【公開シンポジウム】「求められる教育・・学力とモラル」
日 時: 2013年9月14日 (土) 13:30 ~18:00(開場13:20)
会 場: 京都大学基礎物理学研究所 湯川記念館パナソニック国際交流ホール
共 催: 京都大学経済研究所、京都大学統合複雑系科学国際研究ユニット、
国際教育学会(ISE)、特別推進研究「経済危機と社会インフラの複雑系分析」、
同志社大学創造経済研究センター
***************************************************
第一部:「効果的な学習」(13:30 ~15:20)
(敬称略)
13:30~13:45: 村瀬雅俊(京都大学基礎物理学研究所 准教授)
「構造主義再考 -自己・非自己循環理論の視点から-」
13:45~14:00: 中林眞佐男(千里金蘭大学・生涯学習センター 非常勤講師)
「日本の生涯学習に関する考察-アンケート調査に基づいて-」
14:00~14:15 奥村聡(一般社団法人CCCプロジェクト代表理事)
「公立小学校での21世紀型国際教育の実践報告と検証
~ライブ動画を用いた日豪間1対1外国語コミュニケーション授業の実践~」
14:15~14:30 平塚儒子(帝塚山学院大学人間科学部 教授)
「日本の少子化と中国(天津市)の一人っ子政策が社会的行動の発達に与える影響」
休憩(14:30~14:35)
14:35~14:50: 須原秀和(須原英数教室 塾長)
「塾教育」
14:50~15:05: 川越栄子(神戸女学院大学 教授)
「英語スピーチ導入の試み」
15:05~15:20: 村瀬智子(日本赤十字豊田看護大学 教授)
「教育現場におけるメタ認識的学習の意義」
休憩(15:20~15:30)
***************************************************
第二部:「モラルと日本流」(15:30 ~16:30)
(敬称略)
15:30~15:50:若井田正文(東京農業大学、前世田谷区教育委員会教育長)
「『人格の完成を目指して』-世田谷区の取組-」
15:50~16:10: 中村多美子(弁護士)
「法曹養成過程における科学技術知見の学習」
16:10~16:30: 西村和雄(国際教育学会(ISE)会長)
「キャリア形成に規範が果たす役割」
休憩(16:30~16:40)
***************************************************
第三部:パネル・ディスカッション(16:40 ~18:00)
「企業にとっての4つのモラルの重要性」
(敬称略)
司会:八木匡(同志社大学経済学部教授)
パネリスト:
野崎晃平(株式会社豊田自動織機 常務執行役員)
渕上智信(株式会社ガイアシステム 代表取締役会長)
高田誠 (株式会社朝日サステイナビリティ・マネジメント 代表取締役社長)
半田延之(株式会社えがお 取締役 )
☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆
懇親会(18:15~20:00)
(会場:京都大学基礎物理学研究所 湯川記念館パナソニック国際交流ホール ロビー)
☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆
■2.第8回大会(総会、公開シンポジウムおよび懇親会)のお申し込み方法について
国際教育学会(ISE) 第8回大会に参加ご希望の方は、本メール末尾の申込書書式にて、
(1)所属
(2)氏名(ふりがな)
(3)メールアドレスまたはファックス番号
(4)総会、公開シンポジウム、懇親会への出席・欠席
をお書き添えの上、8月30日(金)までに、メールまたはファックスにて下記までお申し込みください。
・FAX: 075-753-7157
・E-mail: ise@sfi-npo.net
・ご入場は無料です。
・会場とアクセス:会場となります京都大学基礎物理学研究所 湯川記念館パナソニック国際交流ホールは、京都大学吉田キャンパスの北部構内にございます。
・京都大学吉田キャンパスへのアクセス:
http://www.kyoto-u.ac.jp/ja/access/campus/
・吉田キャンパスの構内配置図:
http://www.kyoto-u.ac.jp/ja/access/campus/map5r.htm
・吉田キャンパス北部構内マップおよび主な交通機関からのアクセス:
http://www.kyoto-u.ac.jp/ja/access/campus/map6r_n.htm
湯川記念館パナソニック国際交流ホールは11番の建物です。
・最寄りの駅:京阪本線「出町柳」駅から東へ徒歩20分
または京都市営バス「京大農学部前」または「北白川」下車(路線によっては「百万遍」で下車ください。)
・問い合わせ先: 国際教育学会(ISE)事務局(担当:青木)
・TEL: 075-753-7184 E-mail: ise@sfi-npo.net
・ホームページ: http://sfi-npo.net/ise/
・・・・・・・・・・・・・・・・・・・・・・・・・・・・書 式・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
「国際教育学会(ISE) 第8回大会参加申込書」
日時:2013年9月14日(土) 13:00~
会場:京都大学基礎物理学研究所 湯川記念館パナソニック国際交流ホール
(1)所属:
(2)氏名:
(ふりがな)
(3)メールアドレスまたはファックス番号:
(4)出席・欠席の別:
・国際教育学会(ISE)第8回大会総会(13:00 ~13:20)□出席 □欠席
・公開シンポジウム(13:30~18:00) □出席 □欠席
・懇親会(18:15~20:00) □出席 □欠席
総会にご欠席の場合は、必ず下記の委任状にご記入の上ご返送ください。
(賛助会員の皆様は委任状は必要ございません。)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む<11回目>」
● 日時: 2013年9月21日(土) 15:00~17:00
● 会場: 正進社 5階 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い,
数学に対する理解を深めます。聴講者は,自由に質問や感想を発言できます。初めての方でも,参加・聴講は心配ありません。
第11回目は,下巻第10章(主に「ある空想的なゲーム」「コーシーの収束条件」「収束と加減乗除」)
を読みます。
● 講師: 上野 健爾、宮永 望、水谷 一、有田 八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(下)」岩波新書
※通常の1回の講座では,1章ほどを読み進めています。
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にて
お知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第12回予定:10月 くわしい日程は,まだ決まっておりません。
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む<10回目>」
● 日時: 2013年7月13日(土) 15:00~17:00
● 会場: 正進社 5階 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い、数学に対する理解を深めます。
聴講者は,自由に質問や感想を発言できます。
初めての方でも,参加・聴講は心配ありません。
※第9回目の講座から,下巻に入りました。
第10回目は,下巻第9章(主に以下の項目)を読む予定です。
解析幾何学,直線,交わりと結び,円錐曲線,二次曲線
● 講師: 上野 健爾、宮永 望、水谷 一、有田 八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(下)」岩波新書
※通常の1回の講座では,1章ほどを読み進めています。
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にてお知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第11回予定:9月 くわしい日程は,まだ決まっておりません。
数学月間応援の皆様
今年も数学月間(7/22~8/22)が近づきました.
数学月間は,<社会を支えている数学に関心を持とう>という活動です.
この時期に,色々な数学イベントが各地で隆盛になることを願っています.
SGKは初日(7/22)に,<数学月間懇話会>を開催(今年で9年目)しています.
数学に興味があるが専門でない一般および学生が対象です.
どうぞお気軽にご参加ください.
参考:22/7≒π,22/8≒eであることに因んでいます(π,eは数学の基礎定数).
詳しくは,SGK通信(2013-06)をご覧ください.
SGK通信に,水谷一氏の扱う問題を予告掲載しています(高校生参加の予定).
――――――――― プログラム ――――――――――
1.考える楽しみわかる喜び,水谷一(日本数学協会)
2.最小二乗問題の新解法と逆問題への応用, 速水謙(国立情報学研究所)
3.数学月間と数学祭り, 谷克彦(日本数学協会)
――――――――――――――――――――――――――
日時●7月22日,14:00-17:00
会場●東京大学(駒場)数理科学研究科棟002号室
最寄り駅●京王井の頭線「駒場東大前」
参加費●無料
申し込み・問合せ先●日本数学協会,数学月間の会(SGK)
sgktani@gmail.com,谷克彦(SGK世話人)
司会進行は渡邊芳行氏によって平成24年度事業活動報告、同収支決算、同じく25年度事業活動計画、および同収支予算について
慎重にご審議頂き、無事原案通り、全て承認されました。
引き続き、有田八州穂先生、新井紀子先生による特別講演会が行われ、
現在の算数・数学教育の問題点が洗い出されるような感じになり、講演に関し、熱心な質問が寄せられました。
日本数学協会総会議事録(第12回).pdf
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む<9回目>」
● 日時: 2013年6月8日(土) 15:00~17:00
● 会場: 正進社5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い、
数学に対する理解を深めます。聴講者は,自由に質問や感想を発言できます。
初めての方でも,参加・聴講は心配ありません。
※第9回目の講座から,いよいよ下巻の第8章(最初の章)に入ります。
「下巻第8章は,主に以下の項目を読み進めます:
合同式・合同式の計算法・約数の発見法・フェルマーの定理・循環小数」
● 講師: 上野健爾、宮永 望、水谷 一、有田八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(下)」岩波新書
※通常の1回の講座では,1章ほどを読み進めています。
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤宛てに、以下の内容をメール( t-ito@seishinsha.co.jp)にて
お知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第10回予定:7月 くわしい日程は,まだ決まっておりません。
※4月・5月の講座は,都合により,お休みしました。
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む 8回目」
● 日時: 2013年3月16日(土) 15:00~17:00
● 会場: 正進社5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、
数名の先生による読み合わせ講座形式で行い、
数学に対する理解を深めます。聴講者は,自由に質問や
感想を発言できます。
初めての方でも,参加・聴講は全く心配ありません。
※第8回目の講座は,上巻でやり残したこと(おもに第7章の方程式の話)を中心に行います。
過去の資料をお持ちの方は,持参願います。
時間がとれれば,上巻の全体についての質問も受けます。
● 講師: 上野健爾、宮永 望、水谷 一、有田八州穂、
(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(上)」岩波新書
※通常の1回の講座では,1章ほどを読み進めています。
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤宛てに、以下の内容をメール
(t-ito@seishinsha.co.jp)にて
お知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、
塾の先生、学生の方、企業等の方)
● 今後の予定:
第9回予定:5月
くわしい日程は,まだ決まっておりません。
4月の講座は,都合により,お休みします。
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む7回目」
● 日時: 2013年2月16日(土) 15:00~17:00
● 会場: 正進社5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の
先生による読み合わせ講座形式で行い、数学に対する理解を深
めます。聴講者は、自由に質問や感想を発言できます。
※第7回目は,上巻の7章「複素数」の内容を読み進める予定です。
初めての方でも,参加・聴講は全く心配ありません。
● 講師: 上野健爾、宮永 望、水谷 一、有田八州穂、
(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(上)」岩波新書
※通常の1回の講座では,1章ほどを読み進めています。
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤宛てに、以下の内容をメール
(t-ito@seishinsha.co.jp)にてお知らせくださいますよう
お願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、
学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定: 第8回予定:3月16日(土)15時開始予定
日本数学協会・国際教育学会共催
■数学入門講座■
「遠山啓の数学入門を読む<6回目>」
● 日時: 2013年1月26日(土) 15:00~17:00
● 会場: 正進社5階会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の
先生による読み合わせ講座形式で行い、数学に対する理解を深
めます聴講者は,自由に質問や感想を発言できます。
※第6回目は,上巻の6章「円の世界」の内容を読み進める
予定です。
初めての方でも,参加・聴講は全く心配ありません。
● 講師:上野健爾、宮永望、水谷一、有田八州穂、(新井紀子)
● 準備するもの: 遠山啓著「数学入門(上)」岩波新書
※通常の1回の講座では,1章ほどを読み進めています。
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:正進社 伊藤宛てに、以下の内容をメール
(t-ito@seishinsha.co.jp)にてお知らせくださいますようお願い
いたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、
塾の先生、学生の方、企業等の方)
● 今後の予定:
第7回予定:2月16日(土)午後3時開始予定,
第8回予定:3月16日(土)午後3時開始予定
《 2013年新春特別講義 》
四日市大学関孝和数学研究所、東京大学理学研究科素粒子物理国際研究センター、日本数学協会の共催で、
「高校生と社会人のための現代数学・物理学入門講座」 新春特別講義 「方程式の世界」
を下記のように開催しますのでご案内します。
◆ 日時:2013年1月12日(土)・13日(日)
会場:東京大学小柴ホール
(http://www.u-tokyo.ac.jp/campusmap/cam01_00_25_j.html)
― プログラム ―
◆1月12日(土)
13:45~15:00 「方程式の豊かな世界」
講師:上野健爾 (四日市大学 関孝和研究所)
15:15~16:45 「n次方程式を解いてみよう」
講師:桂 利行 (法政大学 理工学部経営システム工学科)
◆1月13日(日)
10:00~11:30 「多項式の割り算と高次連立方程式」
講師:徳永浩雄 (首都大学東京 大学院理工学研究科)
13:00~14:30 「微分方程式の豊かな世界から」
講師:清水勇二 (国際基督大学 教養学部)
14:45~16:15 「素粒子物理と方程式 ―光、電子からヒッグス粒子まで―」
講師:小林富雄 (東京大学 素粒子物理国際研究センター)
● 受講料:学生(含む大学生)無料 / 社会人1,000円
● 参加資格:どなたでも参加できます(部分参加も可)
● 募集人員:約150名(先着順)
● 応募方法:往復はがきに住所、氏名、学校名(学生の場合は学年も)または
勤務先および電話番号明記の上、返信はがきに自分のあて先を書いて下記までお送り下さい。12月20日までに必着のこと。(先着順受付)
〒160‐0022 東京都新宿区新宿2-3-16ライオンズマンション御苑前504号
四日市大学関孝和数学研究所東京分室 新春特別講義係
●問合わせ先:四日市大学関孝和数学研究所東京分室 TEL&Fax 03‐5925‐8347
(宿泊の世話はできかねますのでご了承ください。)
■数学入門講座■
「遠山啓の数学入門を読む<5回目>」
● 日時: 2012年12月15日(土) 15:00~17:00
※11月の講座はありません。
● 会場: 正進社 5階 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い、数学に対する理解を深めます。
※第5回目は,上巻の5章または5~6章の内容を読み進めます。
初めての方でも,参加・聴講は全く心配ありません。
● 講師: 上野 健爾、宮永 望、水谷 一、有田 八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(上)」岩波新書
※通常の1回の講座では,1章~2章ほどを読み進めています。
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にて
お知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
来年からのくわしい日程は,後日メールやHP等でお知らせいたします。
新しい住所は下記のとおりです。
〒160-0011
東京都新宿区若葉1-10
TEL 03-6821-3313
FAX 03-5269-8182
MAIL sugakubunka@gmail.com
■数学入門講座■
「遠山啓の数学入門を読む<4回目>」
● 日時: 2012年10月27日(土) 15:00~17:00
● 会場: 正進社 5階 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い、
数学に対する理解を深めます。
※第4回目は,上巻の1章から4章までをもう一度見直します。
初めての方でも,参加・学習は全く心配ありません。
● 講師: 上野 健爾、宮永 望、水谷 一、有田 八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(上)」岩波新書
※通常の1回の講座では,1章~2章ほどを読み進めています。
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にて
お知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第5回目の日程は,11月下旬を予定しております。くわしい日程は,後日メールやHP等でお知らせいたします。
開催日時:平成24年9月16日(日)
※今年度は都合により1日だけの開催となりました。
会場:東京大学駒場キャンパス 数理科学研究科
10:00 開会挨拶
10:05 講演 『ヒルベルトと現代数学ー生誕150年を記念してー』
講師 上野健爾
(質疑応答含む)
(ポスターセッション)
・武純也 『数詞覆面算とコンピュータ』
・平野年光 『京都東山・安井金比羅宮『算題四季詠』問題の教材化』
・山本景一 『京都東山近辺社寺奉納算額問題教材化の研究』
・松井陽一郎 『 ?線の研究(公式を導く)、?画家にとって数学とは』
・藤森弘章 『2×2行列の解剖と新しい標準形』
・高橋俊彦 『K〜N』
・山本文隆 『ピタゴラス数ネットはなぜ描けるか』
・山本文隆 『逆正接におけるオイラーの公式の一般化』
14:00 熊谷女子高等学校 算脱(継子立て)
14:30 熊谷高等学校 二項定理を利用してパスカルの三角形を描く
15:00 熊谷女子高等学校 あみだくじと置換
15:30 閉会挨拶
「遠山啓の数学入門を読む<3回目>」
● 日時: 2012年9月29日(土) 15:00~17:00
● 会場: 正進社 5階 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い、
数学に対する理解を深めます。
3回目は,上巻の3章を読み合わせる予定です。
● 講師: 上野 健爾、宮永 望、水谷 一、有田 八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(上)」岩波新書
※講座の3回目は,上巻第3章から学び始めます。1回の講座で1章~2章ほど読み進めます。
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にて
お知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第4回目以降の日程は未定です。後日,メールやHP等でお知らせいたします。
当協会の事業活動につきましては、種々ご協力
いただきまして、誠にありがとうございます。
これまで皆様の投稿論文を受け付けておりましたが、
本日を持ちまして財政上の理由より、論文の受付を
終了させていただくこととなりました。
ご理解のほど、よろしくお願い申し上げます。
「遠山啓の数学入門を読む<2回目>」
● 日時: 2012年8月25日(土) 13:00〜15:00
※日程と開始時間が変更となりました。
ご注意願います。
● 会場: 正進社 5階 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い、
数学に対する理解を深めます。
● 講師: 上野 健爾、宮永 望、水谷 一、有田 八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(上)」岩波新書
※講座の2回目は,上巻第2章から学び始めます。1回の講座で1章〜2章ほど読み進めます。
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にて
お知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第3回目以降は,未定でございます。HP等でお知らせいたします。
当協会では、機関誌「数学文化」の発行や数学文化公開講演会の開催などの諸活動を通じて、
数学を学び楽しさをアピールし、数学文化の向上に努めておりますが、
更なる数学文化の向上と数学と数学教育の意義を再確認する運動の一環として、
昨年開催した第4回総会において、毎年7月22日~8月22日の1カ月間を、数学月間とすることを決定し、
関係諸学会等とも協力し、多くの皆様方に数学を学ぶ楽しさをアピールしていくことにいたしました。
つきましては、この月間内(あるいはその前後)に、実施される数学的な行事(例えば、
講演会や出前授業、勉強会、文部科学省が実施している「科学技術・理科大好きプラン」事業である
サイエンス・パートナーシッププログラム(SPP)やスーパーサイエンスハイスクール(SSH)などとの
連携講座、珠算競技大会、展示(覧)会、オープンキャンパスの1企画など)がございましたら、
是非「数学月間に連携した行事」としていただくよう関係の皆様方のご協力をお願いいたします。
当協会宛に「数学月間に連携した行事」としてご連絡いただいた行事は、
数学を学ぶ楽しさを実感できる場として、上記の一覧表により、随時ご案内してまいります。
「数学」は「数我苦」ではなく「数楽」であることを一人でも多くの方々に知ってもらうために、協力してアピールしていきましょう。
(注意1) 22/7=3.14・・・≒π、 22/8=2.7・・・≒e(自然対数の底)にちなんでいる。
(注意2)アメリカでは大統領宣言に基づいて1986年に4月中旬の一週間を数学週間と定め、それ以降、数学月間に拡大して活動が続いている。
<本件連絡先>日本数学協会事務局
〒338−8570
埼玉県さいたま市桜区下大久保255
場所:東大駒場キャンパス,数理科学研究科棟,056号室
プログラム:
●14:10〜15:10
「数理化学の探検−化学の中の数学の世界」
細矢治夫(お茶の水女子大,名誉教授)
●15:20〜16:20
「じゃんけんの必勝法を論じて、あわせて統計的思考に及ぶ」
石黒真木夫(統計数理研究所,名誉教授)
●16:30〜17:00
数学月間について意見交換
日・米・英の数学月間は,どのような活動でしょうか.
「遠山啓の数学入門を読む<1回目>」
● 日時: 2012年6月30日(土)15:00〜17:00
● 会場: 正進社 5階 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(伊藤メール t-ito@seishinsha.co.jp)
(正進社HP http://www.seishinsha.co.jp)
● 講座内容:
岩波新書・遠山啓著の「数学入門(上・下巻)」を、数名の先生による読み合わせ講座形式で行い、数学に対する理解を深める。
● 講師: 上野 健爾、宮永 望、水谷 一、有田 八州穂、(新井 紀子)
● 準備するもの: 遠山啓著「数学入門(上)」岩波新書
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法:
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にて
お知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
● 今後の予定:
第2回 7月28日(土) 15:00〜17:00 「遠山啓の数学入門を読む<2回目>」
など
〒338−8570
埼玉県さいたま市桜区下大久保255
埼玉大学総合研究機構棟520号室
TEL:048−858−3941
FAX:048−851−2134
E-Mail:sugaku@fa2.so-net.ne.jp
日本数学協会・国際教育学会共催
■『第9回 教師と大人のための算数・数学講座(2012)』■
● 日時: 2012年3月17日(土)14:00〜16:30
● 会場: 正進社 5階 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(正進社HP http://www.seishinsha.co.jp)
● 講座内容 「わり算と分数」
・講座の中で、等分除・包含除についても触れます。
● 講師: 有田 八州穂 先生 ほか
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にて
お知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の
方、企業等の方)
● 今後の日程
4月はお休みです。5月以降の予定は分かり次第、ご連絡いたします。
■『第8回 教師と大人のための算数・数学講座(2012)』■
● 日時: 2012年2月18日(土)14:00〜16:30
● 会場: 正進社 5階 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:(03) 5229-7663 小学編集部 伊藤
(正進社HP http://www.seishinsha.co.jp)
● 講座内容 「対称とは何か、対称をどう教えるか」
上野 健爾 先生、有田 八州穂 先生 ほか
● 会場地図: 下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/
● 申し込み方法
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にて
お知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の
方、企業等の方)
● 今後の日程
第9回 3月17日(土)14:00〜16:30予定 「わり算と比」 会場:正進社
教師と大人のための算数・数学講座(2012)
日程・内容
第7回 1月14日(土)14:00〜16:30
正進社 5階 会議室 にて
正進社HP http://www.seishinsha.co.jp
講座内容 「筆算と暗算」
上野健爾、有田八州穂
【申し込み方法】
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp)にてお知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等)
【1月以降のの予定】
第8回 2月18日(土)14:00〜16:30 「対称とは何か、対称をどう教えるか」 正進社にて
第9回 3月17日(土)14:00〜16:30 「わり算と比」 正進社にて
教師と大人のための算数・数学講座(2011)
日程・内容
第5回 11/26(土)14:00〜16:30
正進社 5階 会議室 にて
前半 「算数ができるとは何か」
有田八州穂
後半 「数学がわかるとは何か」
上野健爾、新井紀子 対談
●第5回は、通常通り、正進社にて14時開始です。
第6回 12/17(土)14:00〜16:30
「割合をどう教えるか」 正進社
●第6回の開催場所が正進社に変更されました。
第7回 1/ (土)14:00〜16:30
「筆算と暗算」 正進社
【申し込み方法】
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp)にてお知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等)
11:00-12:30 = 日本数学史の入門
松永良弼の手紙を読む(副所長・小川束)
13:30-15:00 = 関孝和の業績の紹介
関孝和の数学(所長・上野健爾)
15:15-16:45 = 質疑応答
パネルディスカッション
(上野健爾,小川束,研究員・藤井康生)
◉対象: 高校生/大学生/一般
◉費用: 無料(弁当を希望しない場合)
◉お問い合わせ/お申し込み:
電 話 059-340-1927
研究機構事務室(13:30〜16:30)
メール skim@yokkaichi-u.ac.jp
氏名,連絡先,弁当希望の場合はその旨明記ください.
第4回 10/22(土)10:30〜13:00
「平行とは何か、平行をどう教えるか」 正進社
●第4回の開催場所が正進社に、時間が10時30分からに変更されました。
ご注意願います。
第5回 11/26(土)14:00〜16:30
「算数が得意とはどういうことか」 正進社
第6回 12/17(土)14:00〜16:30
「割合をどう教えるか」 正進社
●第6回の開催場所が正進社に変更されました。
第7回 1/ (土)14:00〜16:30
「筆算と暗算」 正進社
【申し込み方法】
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にてお知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
開催日 平成23年9月3日(土)・4日(日)
会場 東京大学駒場キャンパス 数理科学研究科棟 中講義室
参加費 会員:2000円 非会員:4000円 高校生以下無料
3日(土)
14:00 開会挨拶
14:05 特別記念講演 『ガロアが考えたこと 〜生誕200年を記念して〜』
15:50 休憩
16:00 分科会ごとの意見交換
16:30 全体で報告会
16:50 移動
17:00 懇親会(イタリアントマト)
19:00 解散
4日(日)
【一般講演A】
9:30〜9:45 パズルで脳トレ日本の数学力をUPしよう!(携帯iアプリ) 菅野 正人
9:45〜10:00 パズルで脳トレ日本の数学力をUPしよう!(ねこパズル) 菅野 正人
10:00〜10:15 新幹線のカーブはなぜかたむいている? 松井 陽一郎
10:15〜10:30 Five Circles for Pentagon 小梁 修
10:30〜10:45 紙鎖立方体 武 純也
10:45〜11:00 数楽模様 染谷 淳一郎
11:00〜11:15 数学文化と授業実践 宮本 俊光
11:15〜11:30 歴史を踏まえ、きちんとした知識からの分数指導 曽我 昇平
【一般講演B】
9:30〜9:45 ピタゴラス数ネット 山本 文隆
9:45〜10:00 ピタゴラス数から導く素数合同数 山本 文隆
10:00〜10:15 相対論におけるエネルギーの考察 室井 正史
10:30〜10:45 石黒信由の「交式斜乗」について 徳田 建司
10:45〜11:00 京都・東山近辺社寺奉納の算額問題教材化に関する研究
平野年光 ・ 山本景一
11:00〜11:15 ゼータ函数に由来する不思議な等式1+2+3+…= − (1/12)
をめぐる謎解き 杉本 明秀
11:15〜11:30 ωにときめき 1+2+3+…ωの計算 深山 順夫
11:30 お昼休憩
13:00〜13:20 ヤングセッション 計算とは何か(1)埼玉県立熊谷高校 選抜チーム
13:25〜13:45 ヤングセッション 計算とは何か(2)埼玉県立熊谷女子高校 選抜チーム
13:45 休憩
15:50 閉会挨拶
教師と大人のための算数・数学講座(2011)
日程
第3回 9/24(土)14:00〜16:30
第4回 10/22(土)14:00〜16:30
第5回 11/26(土)14:00〜16:30
第6回 12/17(土)14:00〜16:30
第7回 1/ (土)14:00〜16:30
正進社 伊藤 宛てに、以下の内容をメール(t-ito@seishinsha.co.jp )にてお知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
4.この講座をどのようにお知りになったか(初めての方のみ)
5.その他(ご意見・ご要望・ご不明な点等)
当協会では、機関誌「数学文化」の発行や数学文化公開講演会の開催などの諸活動を通じて、数学を学び楽しさをアピールし、
数学文化の向上に努めておりますが、更なる数学文化の向上と数学と数学教育の意義を再確認する運動の一環として、
昨年開催した第4回総会において、毎年7月22日~8月22日の1カ月間を、数学月間とすることを決定し、
関係諸学会等とも協力し、多くの皆様方に数学を学ぶ楽しさをアピールしていくことにいたしました。
つきましては、この月間内(あるいはその前後)に、実施される数学的な行事
(例えば、講演会や出前授業、勉強会、文部科学省が実施している「科学技術・理科大好きプラン」事業である
サイエンス・パートナーシッププログラム(SPP)やスーパーサイエンスハイスクール(SSH)などとの
連携講座、珠算競技大会、展示(覧)会、オープンキャンパスの1企画など)がございましたら、
是非「数学月間に連携した行事」としていただくよう関係の皆様方のご協力をお願いいたします。
当協会宛に「数学月間に連携した行事」としてご連絡いただいた行事は、
数学を学ぶ楽しさを実感できる場として、上記の一覧表により、随時ご案内してまいります。
「数学」は「数我苦」ではなく「数楽」であることを一人でも多くの方々に知ってもらうために、協力してアピールしていきましょう。
(注意1) 22/7=3.14・・・≒π、 22/8=2.7・・・≒e(自然対数の底)にちなんでいる。
(注意2)アメリカでは大統領宣言に基づいて1986年に4月中旬の一週間を数学週間と定め、それ以降、数学月間に拡大して活動が続いている。
<本件連絡先>日本数学協会事務局
〒338−8570
埼玉県さいたま市桜区下大久保255
日時●7月22日,14:00-17:00
内容●
1.サイバー世界のモデリング,北川源四郎(情報・システム研究機構)
2.量子コンピューティングの考え方,荒井隆(防衛大)
3.今年の米国MAMの話題,谷克彦(SGK)
会場●東京大学(駒場)数理科学研究科棟056教室
最寄り駅●京王井の頭線「駒場東大前」
参加費●無料
問合せ先●日本数学協会,数学月間の会(SGK)
sgktani@gmail.com,谷克彦(SGK世話人)
www.sugaku-bunka.org/
−模型を作って算数・数学を楽しみましょう−数楽しましょ!−
日程:平成23年8月13日(土)
時間:(午前) 11:10-11:55
会場:国際基督教大学(ICU) 本館304
対象:主として高校生及び父兄
講師:清水勇二(数学 教授)
「角度をどう教えるか」
●講師:有田八州穂先生・上野健爾先生・岡部恒治先生
●会場:パナソニックセンター東京3F会議室4〜6
※年間スケジュールに沿って開催することになっております。
今後の予定につきましては添付の「2010年度第4土曜大学講座要綱」をご確認くださいますようお願いいたします。
※「2010年度第4土曜大学講座要綱」に、
5.費用:日本数学協会員、国際教育学会員は原則として無料 それ以外は、資料代として、1講座500円いただきます。
と記載しておりますが、現在資料代はいただいておりません。
【申し込み方法】
正進社 鈴木 宛てに、以下の内容をメールにてお知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
4.この講座をどのようにお知りになったか(初めての方のみ)
5.その他(ご意見・ご要望・ご不明な点等)
日 時 3月12日(土) 13:00〜16:00
場 所 コラッセふくしま3階 企画展示室
(JR福島駅西口より徒歩3分)
内 容 「和算inふくしま」
1.歴史や文化財について調べ、紹介するチーム
2.折り紙などのものづくりチーム
3.問題を研究し、普及するチーム
に分かれて、チームごとに和算を楽しみませんか。
持ち物 筆記用具、定規、コンパス、のり、はさみ
案内人 五輪教一
連絡先 藤田理穂 〓090ー5180ー0776
第6回 1月22日(土)14:00〜17:00
「代数的感覚をどう教えるか」
●講師:新井紀子先生・有田八州穂先生・上野健爾先生・岡部恒治先生
●会場:パナソニックセンター東京3F会議室4〜6
※年間スケジュールに沿って開催することになっております。
今後の予定につきましては添付の「2010年度第4土曜大学講座要綱」をご確認くださいますようお願いいたします。
※「2010年度第4土曜大学講座要綱」に、
5.費用:日本数学協会員、国際教育学会員は原則として無料 それ以外は、資料代として、1講座500円いただきます。
と記載しておりますが、現在資料代はいただいておりません。
【申し込み方法】
正進社 鈴木 宛てに、以下の内容をメールにてお知らせくださいますようお願いいたします。
1.参加者名
2.メールアドレス
3.所属(数学協会会員様、国際教育学会会員様、学校の先生、塾の先生、学生の方、企業等の方)
4.この講座をどのようにお知りになったか(初めての方のみ)
5.その他(ご意見・ご要望・ご不明な点等)
場 所 コラッセふくしま 三階 会議室302
(JR福島駅西口より徒歩3分)
内 容 第1部 「和算inふくしま」 10:00〜12:00
元日の福島民友紙に掲載される算額問題に挑戦します。
第2部 「高校生のための数学セミナー」 13:30〜16:00
第1部で取り上げた問題を、高校数学を用いて考え、発展させます。
持ち物 筆記用具、定規、コンパス、はさみ
案内人 五輪教一
連絡先 藤田理穂 〓090ー5180ー0776
『遊ぼう!和算inふくしま―算額絵馬に挑戦―』
日 時 11月28日(日) 10時〜12時
場 所 コラッセふくしま 三階 会議室301
(JR福島駅西口より徒歩3分)
内 容 「 さいなら三角また来て四角」
江戸時代から明治時代にかけて、
福島県は和算がとても盛んな地域でした。
先人たちの足跡をほんの少しだけ、
一緒にたどってみませんか?
ゆっくり、楽しく、おしゃべりしながら…。
持ち物 筆記用具、定規、コンパス、はさみ
案内人 五輪教一
連絡先 藤田理穂 〓090ー5180ー0776
新春特別講義
究極の数「複素数」
日時 2011年1月8日(土)・9日(日)
首都大学東京 南大沢キャンパス(11号館2F204号室)
八王子市南大沢1-1 京王相模原線 南大沢下車
アクセス http://www.tmu.ac.jp/access.html
キャンパスマップ http://www.tmu.ac.jp/university/campus_guide.html
プログラム
1月8日(土)
13:15 -- 15:15「虚の数から究極の数へ」
講師 上野 健爾(四日市大学 関孝和数学研究所)
15:45 -- 17:45「数の織りなす世界」
講師 桂 利行(法政大学 理工学部経営システム工学科)
1月9日(日)
10:00--12;00「変数を複素数にして考えてみる 」
講師 徳永 浩雄(首都大学東京 都市教養学部理工学系数理科学コース )
14:00--16:00「複素数の幾何」
講師 清水 勇二(国際基督教大学 教養学部)
受講料 無料
参加資格 総ての講義に出席可能な者。(宿泊の世話は出来かねますのでご了承下さい。)
募集人員 約150名
応募方法 往復はがきに住所、氏名、学校名(学生の場合は学年も記してく ださい)
または勤務先、および電話番号を明記の上、返信用はがきに応募者の 宛先を書いて
〒338-8570 埼玉県さいたま市桜区下大久保255
埼玉大学総合研究機構棟520号室
日本数学協会事務局 新春特別講義係
に12月10日までに必着のこと。受講者は原則として先着順に受け付けます。返信用はがきは受講票になります。
問合せ先 (Faxでお願いします)
受講に関すること 日本数学協会事務局 「新春特別講義係」 Fax 048-851-2134
会場その他に関すること 首都大学東京都市教養学部理工学系数理科学コース内
徳永 浩雄 Fax 042-677-2481
『遊ぼう!和算inふくしま―算額絵馬に挑戦―』
日 時 10月17日(日) 10時〜12時
場 所 コラッセふくしま 三階 企画展示室B
(JR福島駅西口より徒歩3分)
内 容 江戸時代から明治時代にかけて、
福島県は和算がとても盛んな地域でした。
先人たちの足跡をほんの少しだけ、
一緒にたどってみませんか?
ゆっくり、楽しく、おしゃべりしながら…。
持ち物 筆記用具、定規、はさみ
案内人 五輪教一
連絡先 藤田理穂 〓090ー5180ー0776
《大人のための算数講座》
(「教師のための算数・数学教育講座」を改題)
★講師
上野健爾(四日市大学関孝和数学研究所),岡部恒治(埼玉大学),有田八州穂(多摩市立大松台小学校)ほか
★会場
リスーピア(パナソニックセンター東京)
〒135-0063東京都江東区有明3-5-1
http://risupia.panasonic.co.jp
http://panasonic.co.jp/center/tokyo
★平成22年(2010年)度の予定
時間はすべて14:00〜17:00
第3回:9月26日(日) テーマ「学校教育と暗算」
第4回:10月24日(日) テーマ「無限の不思議さ」
第5回:11月27日(土) テーマ「図形感覚を育む」
第6回:1月22日(土) テーマ「代数的感覚をどう教えるか」
第7回:2月27日(日) テーマ「角度をどう教えるか」
第8回:3月26日(土) テーマ「関数をどう教えるか」
東京珠算教育連盟 特別会員部会 部長
ビエンナーレ展グラフイック&ドローイング部門最高賞受賞)

ただし、以下の形式でお願いします。
ポスターセッションの申し込み期日は7月31日までとします。当日
本人が来られない場合は、この日までにポスターを事務局宛に
ご送付ください。
1. 1枚の模造紙(788×1091mm以下の大きさ)に最初にタイトル
と名前と連絡先を書く。
2. 発表内容については、形式は問いませんが、ほかの方が理解
しやすいように発表したいことをまとめてください。
3. カラーを用いたり、写真等を使うことは差し支えありませんが、
あまり立体的に突出しないようお願いします。
4. 原則として本人が掲示し、説明をすること。ただし、送付する
ことも認めます(この場合も参加費を払ってください)。
なお、掲示場所は、事務局にご一任ください。
2010年度第4土曜大学「大人のための算数講座」(旧称:教師のための算数・数学講座)
講 座 要 綱
1. 主催団体:日本数学協会 国際教育学会 パナソニックセンター東京「リスーピア」
2. 開講日:原則として、毎月第4土曜日14:00〜17:00
3. 場所:原則として、臨海線国際展示場前 「リスーピア」会議室
(江東区有明3−5−1 ?:03−3599−2463)
4. 講師:上野健爾(京都大名誉教授・四日市大関孝和数学研究所所長)
岡部恒治(埼玉大教授)
新井紀子(国立情報学研究所教授)
有田八州穂(公立小学校教員・四日市大関孝和数学研究所研究員)
(他に、そのときの、テーマに応じてふさわしい専門家を呼びます)
5. 費用:日本数学協会員、国際教育学会員は原則として無料 それ以外は、資料代として、
1講座500円いただきます。
6. 事務局:KK.正進社におきます。(担当:鈴木裕美子)
(文京区関口1−17−8 ?:03−5229−7663 E-mail:suzuki@seishinsha.co.jp)
7. 今年度の講座予定
第1回 7月4日(日)「新指導要領の重点、算数的活動・数学的活動をどうするか」(済)
第2回 7月24日(土)「緊急講座、教育の電子化にどう対応するか――電子教科書と電子黒板――電子黒板の試用があります」
(8月21日(土)22日(日)東京大学数理科学研究科棟(駒場)で日本数学協会の年会
があり、特別講演「数学教科書が危ない――数学教科書の変遷」(上野健爾)がありま
す。特別講座としますので、これにも、参加ください。)
第3回9月26日(日)「学校教育と暗算」
第4回10月24日(日)「無限の不思議さ」
第5回11月27日(土)「図形感覚を育む」
第6回1月22日(土)「代数的感覚をどう教えるか」
第7回2月27日(日)「角度をどう教えるか」
第8回3月26日(土)「函数をどう教えるか」
当協会では、機関誌「数学文化」の発行や数学文化公開講演会の開催などの諸活動を通じて、数学を学び楽しさをアピールし、
数学文化の向上に努めておりますが、更なる数学文化の向上と数学と数学教育の意義を再確認する運動の一環として、
昨年開催した第4回総会において、毎年7月22日~8月22日の1カ月間を、数学月間とすることを決定し、
関係諸学会等とも協力し、多くの皆様方に数学を学ぶ楽しさをアピールしていくことにいたしました。
つきましては、この月間内(あるいはその前後)に、実施される数学的な行事
(例えば、講演会や出前授業、勉強会、文部科学省が実施している「科学技術・理科大好きプラン」事業である
サイエンス・パートナーシッププログラム(SPP)やスーパーサイエンスハイスクール(SSH)などとの
連携講座、珠算競技大会、展示(覧)会、オープンキャンパスの1企画など)がございましたら、
是非「数学月間に連携した行事」としていただくよう関係の皆様方のご協力をお願いいたします。
当協会宛に「数学月間に連携した行事」としてご連絡いただいた行事は、
数学を学ぶ楽しさを実感できる場として、上記の一覧表により、随時ご案内してまいります。
「数学」は「数我苦」ではなく「数楽」であることを一人でも多くの方々に知ってもらうために、協力してアピールしていきましょう。
(注意1) 22/7=3.14・・・≒π、 22/8=2.7・・・≒e(自然対数の底)にちなんでいる。
(注意2)アメリカでは大統領宣言に基づいて1986年に4月中旬の一週間を数学週間と定め、それ以降、数学月間に拡大して活動が続いている。
<本件連絡先>日本数学協会事務局
〒338−8570
埼玉県さいたま市桜区下大久保255
埼玉大学総合研究機構棟520号室
TEL:048−858−3941
FAX:048−851−2134
E-Mail:sugaku@fa2.so-net.ne.jp
日時●7月22日,14:00−17:00
内容●「手と目で鑑賞,数学曲面と多面体ー直感幾何学ふたたび」(手嶋吉法,産総研),
触って鑑賞の時間もあります,惑星やプランクトンにも触れます. ,
「自由に触って鑑賞」,「教育数学の試み」(岡本和夫,大学評価・学位授与機構),
「数学月間に期待するもの」(意見交換),
会場●東京大学駒場キャンパス,数理科学研究科棟056号教室
最寄り駅●駒場東大前
参加費●無料
申込み&問合せ先●日本数学協会幹事SGK世話人,谷克彦,
sgktani@gmail.com,tel/fax03-3383-2978
お茶の水女子大学数学教室及び数学科同窓会 共催
日本数学協会数学月間(7月22日から8月22日)連携事業
場 所
会 費
お茶の水女子大学准教授
1.「√5 ってなんだろう」(続編)
日時:平成22年7月24日(土) 13:00〜16:00
場所:コラッセふくしま(JR福島駅西口より徒歩3分)
対象:高校生以上
定員:20名(当日受付)
会費:200円(会場費)
2.「対称性をさぐる」(第10回 安達太良高原セミナー)
日時:平成22年8月11日(水)・12日(木) 両日とも10:00〜16:00
場所:福島県郡山市中央公民館(JR郡山駅西口よりバス10分)
対象:高校生以上
定員:30名(当日受付)
会費:1,000円(昼食は各自ご用意ください)
お問合せ先:五輪教一(福島県立橘高校 024-535-3395)
上智大学大学院理工学研究科数学領域/理工学部数学科
場所: 上智大学3 号館325 教室
(http://www.sophia.ac.jp/J/sogo.nsf/Content/campusmap yotsuya をご覧下さい。)
プログラム
• 13:30-14:30
講演者: 筱田健一 (上智大学理工学部教授)
題目: 数学と対称性
• 15:00-16:00
講演者: 清水清孝 (上智大学理工学部教授)
題目: 物理学と対称性
◎ この講演会は非専門家向で, 一般の方の参加を歓迎します。参加費は無料です。
連絡先: 筱田健一(Tel: 03-3238-3466, Email: shinoda@mm.sophia.ac.jp
大阪大学理学部数学教室では、数学に興味を持つ若い皆さんのために、現代数学の様相と数学研究の実際、自然科学や社会科学に及ぼす数学の影響、文化としての数学の在り方などについて、
多角的な視点から易しく解説する公開講座を以下の要領で開催します。受講料は無料です。
平成22年度の詳細
日程:平成22年8月19日(木)
時間:午前10時〜11時50分
会場:大阪大学豊中キャンパス 理学部F棟102
対象:主として高校生(引率の先生も含む)
講師:有木進(情報基礎数学専攻 教授)
詳細は:http://www.math.sci.osaka-u.ac.jp/koukai/
−−−−−−−−−−−−−−−−−−−−−−−
内容:行列の話
高校で行列を習いますが,行列が現代科学で活躍している様子の紹介.
可制御性,可観測性の概念を中心に高校生対象
http://www.collegium.or.jp/~kutomi/index.php
〜小学校・中学校・高校における算数的活動・数学的活動とは〜
●講師:有田八州穂先生・上野健爾先生・岡部恒治先生(・新井紀子先生)
●日時:7月4日(日) 10:00〜12:00
●場所:パナソニックセンター東京 2階 会議室4〜6
●地図:http://panasonic.co.jp/center/tokyo/access/index.html
●受講料:無料
● 申し込み方法:メールかファックスで「正進社 鈴木 宛」にお申し込みください。
Fax: 03(5229)7987
Mail: suzuki@seishinsha.co.jp
●「作ろう算数 創ろう文化」開催のお知らせ 福島支部
日時:平成22年5月29日(土) 13:00〜16:00
場所:コラッセふくしま(JR福島駅西口より徒歩3分)
内容:「√5 ってなんだろう」
対象:高校生以上
定員:16名(当日受付)
会費:200円(会場費)
お問合せ先:五輪教一(福島県立橘高校 024-535-3395)
算数的活動・数学的活動とは
新しい学習指導要領も算数の教科書の検定が、先ごろ発表になりました。
ところが、今回強調されている算数的活動・数学的活動について、現場では
手探り状態です。また、「景気対策」の掛け声のもと、算数的・数学的活動と
対極をなすような「教科書のディジタル化を早期に実現しよう」という動きも
見え隠れしています。
今回のシンポジウムではこの意味と問題点を考えていきたいと思います。
関数の教材(ファンクション・シューター)が新たに加わったRiSuPiaの見学
がてら、おいでください。
●日本数学協会,後援:パナソニックセンター・リスーピア
日時●5月23日(日) 14:30〜17:00
パネラー●上野健爾(数学協会会長),岡部恒治(埼玉大),有田八州穂
会場●パナソニックセンター・リスーピア
最寄り駅●りんかい線「国際展示場駅」
参加費●無料
シンポジウムのご案内
−−−今求められている学力とは何か−−−
・パネリスト
前京都大学大学院理学研究科教授 上 野 健 爾
埼玉大学経済学部教授 岡 部 恒 治
京都大学経済研究所所長・教授 西 村 和 雄
多摩市立多摩第二小学校教諭 有 田 八 州 穂
3 謝辞 多摩市立多摩第二小学校校長 後 藤 信 行
◆共催 日本数学協会 国際教育学会
●日時:平成22年3月14日(日) 「π の日」 9:00〜17:00
●場所:福島県郡山市中央公民館(JR郡山駅西口よりバス10分)
●内容:1.π 生地の作り方 2.π の食べ方 (五輪教一)
3.√π の作り方 4.黄金ピタゴラスパズルの楽しみ方 (小梁 修)
●対象:高校生以上
●会費:1,000円(昼食は各自ご用意ください)
お問い合わせ先:024−535−3395(福島県立橘高校内 五輪教一)
●期日:11月29日(日) 場所:郡山市中央公民館(JR東北郡山駅西口 徒歩23分)
9:00〜12:00 「市民のための数学セミナー」
●期日:12月23日(水) 天皇誕生日
場所:コラッセふくしま 3階会議室302B(JR東北福島駅西口 徒歩3分)
9:30〜12:30 「市民のための数学セミナー」
13:30〜15:30 「親子で作ろう いちにっ算数」
お問い合わせ:024−535−3395(福島県立橘高校内 五輪教一)
■『教師のための算数・数学教育講座(第13回)』■
● 内容:「円周率とは何か(2)」
● 講師:有田八州穂先生・上野健爾先生・他(未定)
● 主催:日本数学協会、国際教育学会(ISE)
● 日時:12月5日(土) 14:00〜
● 場所:株式会社 正進社 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:03(5229)7663 小学編集部
● 受講料:無料
● プログラム
1,『円周率とは何か(2)』 上野 健爾 先生
2,『円周率をどう教えるか(2)』 有田 八州穂 先生
● 申し込み方法:メールかファックスで「正進社 鈴木 宛」にお申し込みください。
Fax: 03(5229)7987
Mail: suzuki@seishinsha.co.jp
● 会場地図:下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/index.html
講師:上野健爾(四日市大学関孝和数学研究所)
「ガロアの夢」
15:45〜17:45
講師:桂 利行(法政大学理工学部経営システム工学科)
「ガロア体と符号ー携帯電話はなぜ聞こえるー」
講師:徳永浩雄(首都大学東京 都市教養学部理工学系数理科学コース)
「ガロア理論をめぐって I」
14:00〜16:00
講師:清水勇二(国際基督教大学教養学部)
「ガロア理論をめぐってII」
(八王子市南大沢1−1京王相模原線南大沢下車)
アクセス http://www.tmu.ac.jp/access.html
キャンパスマップ
日本数学協会事務局「新春特別講義係」
会場・その他に関すること
首都大学東京 都市教養学部理工学系数理科学コース内
徳永浩雄 Fax 042ー 677ー 2481
● 内容:「円周率とは何か」
● 講師:新井紀子先生・有田八州穂先生・上野健爾先生・岡部恒治先生
● 主催:日本数学協会、国際教育学会(ISE)
● 日時:10月31日(土)10:00〜13:00
● 場所:株式会社 正進社 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:03(5229)7663 小学編集部
● 受講料:無料
● プログラム
1,『円周率とは何か』 上野 健爾 先生
2,『円周率をどう教えるか』 有田 八州穂 先生
3,コメント 新井 紀子 先生・岡部 恒治 先生
● 申し込み方法:メールかファックスで「正進社 鈴木 宛」にお申し込みください。
Fax: 03(5229)7987
Mail: suzuki@seishinsha.co.jp
● 会場地図:下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/index.html
期日:10月18日(日)
場所:コラッセふくしま 3階企画展示室D (JR東北福島駅西口 徒歩3分)
9:30〜12:30 「市民のための数学セミナー」
13:30〜15:30 「親子で作ろう いちにっ算数」
お問い合わせ:024−535−3395(福島県立橘高校内 五輪教一)
期日:9月23(水) 秋分の日
場所:コラッセふくしま 3階会議室302B(JR東北福島駅西口 徒歩3分)
9:30〜12:30 「市民のための数学セミナー」
13:30〜15:30 「親子で作ろう いちにっ算数」
お問い合わせ:024−535−3395(福島県立橘高校内 五輪教一)
● 主催:日本数学協会、国際教育学会(ISE)
住所:東京都文京区関口1-17-8
問い合わせ先:03(5229)7663 小学編集部
日頃より、当協会の各種事業につきましては、種々ご協力をいただきありがとうございます。
さて、設立から8年目を迎えた当協会では、本年8月22日(土)と23日(日)の2日間、
東京大学駒場キャンパスの数理科学研究科棟(http://www.ms.u-tokyo.ac.jp/access/index.html)で
第7回年次大会を開催いたします。
なお、数理科学研究棟へは、正門から行くこともできますが、東大駒場前駅の改札口を出て右に降り、
線路沿いを渋谷方面に戻り、ぶつかったところで左折し線路を渡って、最初に右に見える建物を目指すのが
近道です。これは、旧矢内原門を通過する道です。
【参加費】〈会員〉2000円、〈非会員〉4000円
(高校生以下は無料です。)
*懇親会は会員、非会員に関わらず3000円です。
プログラムは以下の通りです。
プログラム(予定)
8月22日(土)
8月23日(日)
一般講演A 座長:有田・逸見
一般講演B 座長:亀井・河野
第7回年次大会における講演(発表)希望者の募集について
日頃より、当協会の各種事業につきましては、種々ご協力をいただきありがとうございます。
さて、設立から8年目を迎えた当協会では、本年8月22日(土)と23日(日)の2日間、
東京大学駒場キャンパスで第7回年次大会を開催いたします。
つきましては、この年次大会において、日頃の研究成果の発表を希望される方を募集いたしますので、
ご多忙のところ誠に恐縮ですが、発表を希望される方は、下記にご留意いただき、下記にあります「講演申込書」に所要事項をご記入のうえ、
「講演予稿」と併せて、7月1日(水)までに事務局宛にご送付くださいますようお願いいたします。
今年度も年次大会では、一般会員の方の発表に加え、学生(中学や高校、高専)の方の発表の場(ヤング・セッション)も設けますので、奮ってお申し込みください。
この年次大会の参加料は、会員が2,000円、非会員が4,000円を予定しています(高校生以下の学生の方は無料です)。
タイムスケジュール等は、決定次第、改めてホームページ等でご案内いたします。
記
1.講演時間は、15分以内としてください。
2.講演予稿は、別添の「講演予稿フォーム」(見本)を参考にして作成してください。
(1)A4判4枚以内に、まとめてください(図表等も含みます)。
(2)ページ番号(1〜4ページ)は、鉛筆書きでお願いします。
(3)「予稿集」として、そのまま印刷できるように、黒インクで記入(または印刷)してください。これを版下原稿と考えてください。
(4)ヤング・セッションの講演予稿の記載フォームは、特に指定しませんが、
上記の講演予稿フォーム(見本)を参考に、A4判4枚以内で作成してください。講演時間は、15分以内です。
<本件担当>
日本数学協会事務局
〒338−8570
埼玉県さいたま市桜区下大久保255
埼玉大学総合研究機構棟520号室
TEL:048−858−3941
FAX:048−851−2134
E-Mail:sugaku@fa2.so-net.ne.jp
URL:./nc1Files
期日:7月20日(月)海の日
場所:コラッセふくしま 3階会議室302B(JR東北福島駅西口 徒歩3分)
9:30〜12:30 「市民のための数学セミナー」
13:30〜15:30 「親子で作ろう いちにっ算数」
お問い合わせ:024−535−3395(福島県立橘高校内 五輪教一)
● 内容:「比とは何か?」
● 講師:新井紀子先生・有田八州穂先生・上野健爾先生・岡部恒治先生
● 主催:日本数学協会、国際教育学会(ISE)
● 日時:7月4日(土) 10:00〜12:30
● 場所:株式会社 正進社 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:03(5229)7663 小学編集部
● 受講料:無料
●
2,『比をどう教えるか』 有田 八州穂 先生
3,コメント 新井 紀子 先生・岡部 恒治 先生
● 内容:「式とは何か」
● 主催:日本数学協会、国際教育学会(ISE)
● 日時:6月6日(土) 13:30〜16:00
● 場所:株式会社 正進社 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:03(5229)7663 小学編集部
● 受講料:無料
● プログラム
1,『式とは何か』 上野 健爾 先生
2,『式をどう教えるか』有田 八州穂 先生
3,コメント 新井 紀子 先生・岡部 恒治 先生
● 申し込み方法:メールかファックスで「正進社 鈴木 宛」にお申し込みください。
Fax: 03(5229)7987
Mail: suzuki@seishinsha.co.jp
● 会場地図:下記の正進社ホームページにてご確認下さい。
http://www.seishinsha.co.jp/company/index.html
今年は『分数ができない大学生』が出版されてから10年になります。
10年前、おりしも改定されていた学習指導要領では、実際にはゆとりがない「ゆとり教育」がその頂点に達しつつありました。
総合的な学習の時間が大きく導入される一方で、教科の時間は大幅に削減されました。
そのあおりで、算数では計算がさらに軽視され、中学・高校の理科の授業への障害の懸念すら出てきました。
しかし、『分数ができない大学生』が、「一流大学でさえ、小学生の計算で躓く学生が 2割もいる」などの実証的な問題提起をしてから、流れが一変しました。
今回の学習指導要領の改訂は、その中で行われており、以前よりも教科の時間の回復がなされています。
今回のシンポジウムは、『分数ができない大学生』の出版前後の舞台裏や、
「分数計算ができないだけが問題なのか。」「筆者たちは総合的学習に反対なのか。」のような疑問にも答えていきます。
これからの教育のあり方を皆さんとともに考え、積極的な議論を繰り広げていきます。
日時:平成21年5月23日(土)13:30〜15:30
会場:パナソニックセンター東京 リスーピアホール
http://panasonic.co.jp/center/tokyo/access/
司会:岡本和夫
http://risupia.panasonic.co.jp/ev_html/ev090428_symposium.html
なお、数学協会事務局でもお問い合わせ等ができます。
田村氏は日本数学協会創設以来副会長として、珠算界と数学界の橋渡し役を担っていただきましたが、
2月11日に惜しまれながらご逝去なされました。ご冥福をお祈りします。
なお、平服でご参加くださるようお願いします。
「作ろう算数 創ろう文化」開催のご案内(福島支部)
期日:5月31日(日)
場所:コラッセふくしま 3階会議室B(JR東北福島駅西口 徒歩3分)
9:30〜12:30 「市民のための数学セミナー」
13:30〜15:30 「親子で作ろう いちにっ算数」
お問い合わせ:024−535−3395(福島県立橘高校内 五輪教一)
「作ろう算数 創ろう文化」開催のご案内
期日:4月18日(土
場所:コラッセ福島 3階企画展示室D(JR東北福島駅西口 徒歩3分)
9:30〜12:30 「市民のための数学セミナー」
13:30〜15:30 「親子で作ろう いちにっ算数」
お問い合わせ:024−535−3395(福島県立橘高校)
日本数学協会・国際教育学会(ISE)共催の、
『教師のための算数・数学教育講座』第6回を開催することになりましたのでご案内申し上げます。
● 内容:「小数とは何か?」
● 講師:新井紀子先生・有田八州穂先生・上野健爾先生・岡部恒治先生
● 主催:日本数学協会、国際教育学会(ISE)
● 日時:2月11日(水) 13:00〜16:00
● 場所:株式会社 正進社 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:03(5229)7663 小学編集部
● 受講料:無料
● 申し込み方法:メールかファックスで「正進社鈴木宛」にお申し込みください。
Fax: 03(5229)7987
Mail: suzuki@seishinsha.co.jp
● プログラム
1,『小数とは何か』 上野健爾先生
2,『小数をどう教えるか』 有田八州穂先生
3,前回のアンケートに対する答え
4,コメント 新井紀子先生・岡部恒治先生
日本数学協会・国際教育学会(ISE)共催の、『教師のための算数・数学教育講座』第5回を開催することになりましたのでご案内申し上げます。
● 内容:「分数とは何か」
● 講師:新井紀子先生・有田八州穂先生・上野健爾先生・岡部恒治先生
● 主催:日本数学協会、国際教育学会(ISE)
● 日時:12月6日(土) 9:00〜12:00
● 場所:株式会社 正進社 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:03(5229)7663 小学編集部
● 受講料:無料
● 申し込み方法:メールかファックスで「正進社 鈴木 宛」にお申し込みください。
Fax: 03(5229)7987
Mail: suzuki@seishinsha.co.jp
● プログラム
1,『分数とは何か』 上野健爾先生
2, コメント 新井紀子先生
3,『分数をどう教えるか』 有田八州穂先生
4, コメント 岡部恒治先生
期日:12月14日(日)
内容: 9:30〜12:30 市民のための数学セミナー
13:30〜15:30 「作ろう算数 創ろう文化」ワークショップ
場所:コラッセ福島3階 会議室302B(JR東北福島駅西口より徒歩3分)
◆第8回安達太良高原セミナー を開催します
日時 平成21年1月10日(土)〜11日(日) 1泊2日
内容 ピタゴラスからフェルマーまで
会場 あだたらふれあいセンター(二本松市岳温泉2-66-2)
最寄り駅 JR東北本線「二本松駅」
対象 高校生を対象としていますが,
数学に関心のある方ならどなたでも参加できます.
定員 20名程度
参加費 学生6000円,一般10000円(1泊3食付)
申込み・問合せ先 福島県福島市宮下町7-41 福島県立橘高校 五輪教一
tel 024-535-3395 gowa.kyoichi@pt43.fks.ed.jp
日時 平成20年11月29日(土)13:30〜16:00
関孝和没後300年記念懸賞問題 成績優秀者
●関・ベルヌーイ数問題 (優秀賞は順不同)
最優秀賞: 石川恒男 (大阪工大教員)
優秀賞 : 阿部翠空星 (鹿児島大学生)
荒田実樹 (富山県立砺波高校1年)
石井俊全 (出版社社員)
内田達夫
成田 收 (高校教員)
藤岡優太 (高校教員)
●異形同術問題 (準グランプリは順不同)
[一般総合]
グランプリ : 竹石遼平 (山形東高校2年)
準グランプリ: 栗原小百合(東京農業大学生)
宮川敏之
久富 望
[高校生の部]
グランプリ : 竹石遼平 (山形東高校2年)
準グランプリ: 古谷駿幸 (山形東高校2年)
佐藤祐路 (山形東高校2年)
羽角 透 (山形東高校3年)
[中学生の部]
グランプリ : 黒住篤優 (灘中2年)
桑田慎也 (三木学園白陵中2年)
準グランプリ: 金子隆之 (安田学園2年)
[小学生の部]
グランプリ : 松阪龍文 (精華小学校6年)
準グランプリ: 野村健斗 (茅ヶ崎小6年)
㈫の最優秀賞: 蒲田さやか (藤沢市立高谷小4年)
[特別賞——親子で数楽賞]: 蒲田さやか・みどり
[特別賞——粒揃いで賞] : 山形東高校数学部
日本数学協会・国際教育学会(ISE)共催の、『教師のための算数・数学教育講座』
第4回を開催することになりましたのでご案内申し上げます。
● 内容: 「面積について」
● 講師: 有田八州穂先生・上野健爾先生・岡部恒治先生
● 主催: 日本数学協会、国際教育学会(ISE)
● 日時: 10月13日(月) 9:00〜12:00
● 場所: 株式会社 正進社 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:03(5229)7663 小学編集部
● 受講料: 無料
● 申し込み方法: メールかファックスで「正進社 鈴木 宛」
にお申し込みください。
Fax: 03(5229)7987
Mail: suzuki@seishinsha.co.jp
● 会場地図: 下記のURL(正進社ホームページ「会社案内」)からご覧いただけます。
http://www.seishinsha.co.jp/company/index.html
.
● ホームページ: http://sfi-npo.net/ise/i-news.html
さて、設立から7年目を迎えた当協会では、本年8月23日(土)と24日(日)の2日間、
東京大学駒場キャンパスの数理科学研究科棟(http://www.ms.u-tokyo.ac.jp/access/index.html)で第6回年次大会を開催いたします。
東大駒場前駅の改札口を出て右に降り、線路沿いを渋谷方面に戻り、ぶつかったところで左折し線路を渡って、
最初に右に見える建物を目指すのが近道です。これは、旧矢内原門を通過する道です。
13:00 開会挨拶 上野会長
13:05 特別講演1 佐藤賢一(電気通信大)
「関孝和の人物像をめぐって---最近の研究から」
14:15 特別講演2
15:45 分科会ごとの意見交換
16:15 全体会
16:45 終了
17:00 懇親会 イタリアントマト
19:00 解散
8月24日(日)
9:00 受付開始
11:30 休憩
11:40 臨時総会
12:00 お昼
13:00 ヤング・セッション(20分ずつ)
岐阜県立岐山高等学校3年数学研究部
谷原好紀、片桐颯也、村瀬将規
慶應義塾普通部 3年 片山陸
『教師のための算数・数学教育講座(第3回)』のご案内
日本数学協会・国際教育学会(ISE)共催の、『教師のための算数・数学教育講座』
第3回を開催することになりましたのでご案内申し上げます。
● 内容: 「計算とは何か」
● 講師: 新井紀子先生・有田八州穂先生・上野健爾先生
● 主催: 日本数学協会、国際教育学会(ISE)
● 日時: 6月29日(日) 9:00〜12:00
● 場所: 株式会社 正進社 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:03(5229)7663 小学編集部
● 受講料: 無料
● 申し込み方法: メールかファックスで「正進社 鈴木 宛」
にお申し込みください。
Fax: 03(5229)7987
Mail: suzuki@seishinsha.co.jp
● 会場地図: 下記のURL(正進社ホームページ「会社案内」)からご覧いただけます。
http://www.seishinsha.co.jp/company/index.html
.
● プログラム:
1,『計算とは何か』 9:00〜 9:30 上野健爾先生
9:30〜10:30 新井紀子先生
2,『計算をどう教えるか』 10:40〜11:40 有田八州穂先生
3,コメント・質疑応答 11:40〜12:00 岡部恒治先生 他
● ホームページ: http://sfi-npo.net/ise/i-news.html
日本数学協会・国際教育学会(ISE)が共催して、『教師のため
の数学教育講座』を開催することになりましたのでご案内申し上げます。
● 内容:「数とは何か」
● 講師:有田八州穂・上野健爾
● 主催:日本数学協会、国際教育学会(ISE)
● 日時:5月25日(日) 9:00〜12:00
● 場所:株式会社 正進社 会議室
住所:東京都文京区関口1-17-8
問い合わせ先:03(5229)7663 小学編集部
● 受講料:無料
● 申し込み方法:メールかファックスで「正進社 鈴木 宛」
にお申し込みください。
Fax: 03(5229)7987
Mail: suzuki@seishinsha.co.jp
● 会場地図:
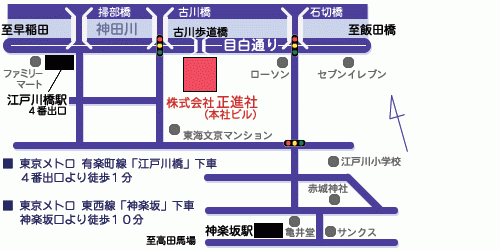
● 内容:「新しい指導要領で算数・数学教育の内容はどう変わるのか?」
● 講師:有田八州穂・上野健爾
● 主催:日本数学協会、国際教育学会(ISE)
● 日時:4月26日(土) 9:00〜12:00
● 場所:株式会社 正進社 会議室
住所:東京都文京区関口 1-17-8
問い合わせ先:03(5229)7663 小学編集部
● 受講料:無料
● 申し込み方法:メールかファックスで「正進社 鈴木 宛」
にお申し込みください。
Fax: 03(5229)7987
Mail: suzuki@seishinsha.co.jp
| 日 | 月 | 火 | 水 | 木 | 金 | 土 |
29 | 30 | 1 | 2 | 3 | 4 | 5 |
6 | 7 | 8 | 9 | 10 | 11 | 12 |
13 | 14 | 15 | 16 | 17 | 18 | 19 |
20 | 21 | 22 | 23 | 24 | 25 | 26 |
27 | 28 | 29 | 30 | 31 | 1 | 2 |


